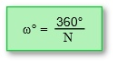Das Fine-Tuning von Bewegungen eines Activity Bot kann sehr trickreich sein; besonders dann, wenn er bestimmte Vorgabemuster wie Dreiecke, Kreise, Hexagone o.ä. abfahren soll.
Der Inhalt dieses Abschnitts lässt sich auch als anwendungsnahe Übung im Mathematikunterricht in der letzten Mittelstufenklasse einsetzen. Die Grundlagen über trigonometrische Funktionen sowie der Cosinussatz sollten bekannt sein.
1 - Berechnung von Drehwinkeln
In diesem Abschnitt wird erklärt, wie man mit einem Parallax Activity Bot mit Differentialantrieb Polygone und Kreisbewegungen ausführt. Wir starten mit einer Einführung in die dafür notwendige Mathematik und setzen diese dann in konkrete Programmbeispiele unter SimpleIDE um. Die hier vorgestellte Mathematik lässt sich natürlich auch auf anderen Robotern mit Differentialantrieb umsetzen; gegebenenfalls müssen die dazu notwendigen Programme modifiziert werden.
Wie lässt sich eine Drehbewegung programmieren? Dazu muss zunächst einmal das Problem an Hand der vorliegenden Hardware (Roboter) genauer studiert werden. Am Ende solltest du dann in der Lage sein, einen Roboter so zu programmieren, dass er sich in eine bestimmte Richtung dreht (im oder entgegen dem Uhrzeigersinn) und das in einem Winkelbereich Omega von 0° bis 360°.
2 - Drehung um ein bestimmtes Winkelmaß
Im Kapitel Activity Bot Propeller - Einfache Bewegungen, Abschnitt 3 - Gerade, Strecken, Drehungen und Encoder Ticks wurde gezeigt, dass der Befehl
-
drive_goto(26, -25)
den ActivityBot um 90° nach rechts dreht. Schauen wir uns dieses Beispiel etwas genauer an und versuchen wir daraus eine mathematische Formel abzuleiten, die uns berechnen lässt, wieviele Ticks bei einem bestimmten Drehwinkel Omega notwendig sind.
Wir wissen aus vorherigen Übungen, dass sich der ActivityBot bei einer Drehung im Stand pro Tick um 3,25mm bewegt. Wenn sich nun der Roboter um eine bestimmte Strecke drehen soll, dann kann die zurückgelegte Bogenstrecke angegeben und daraus die für diese Drehung notwendige Anzahl an Ticks über (1) berechnet werden.
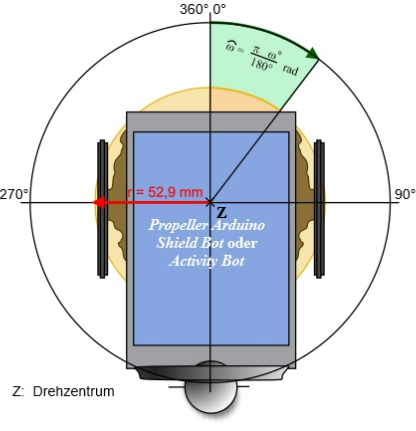
Wenn der ActivityBot sich um seine Achse dreht, beschreiben seine Räder einen Kreis mit Radius r = 52,9mm. In Abb. 1 entspricht das dem gelben Kreis. Dreht sich der Roboter nur um 1Radiant (rad), dann bewegt sich jedes Rad um eine Strecke, die von seinem Abstand r zum Drehzentrum Z abhängt. Es gilt allgemein:
-
je größer der Abstand von Z, desto größer die zurückgelegte Strecke auf dem Kreisbogen. -
der Winkel, der auf dem Kreisumfang die Länge des Radius abgreift, beträgt 1 rad.
Bei einem Abstand r der Räder vom Drehzentrum Z von 52,91mm, wird eine Drehung von 1 Radiant nach (1) mit
-
52,91mm/3,25mm = 16,2769 Ticks
erreicht.
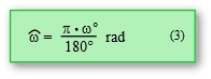
Will man lieber mit Winkelmaßen arbeiten, muss von Radiant in Grad umgerechnet werden. Der Zusammenhang wird in (3) dargestellt.
Daraus ergibt sich sofort (4)
... und wenn man jetzt noch die festen Zahlenwerte multipliziert, ergibt sich die griffige Formel (5)
Nach (5) lässt sich jetzt leicht berechnen, wieviele Ticks ein Rad ausführen muss, damit es sich um einen Winkel Omega dreht.
Beispiel
Bei einer 90°-Drehung ergeben sich nach (5):
-
90*0,2840... = 25,56.. -> 26 Ticks.
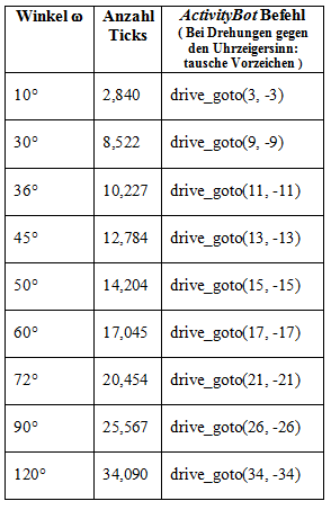
Einfacher ist es, sich eine Tabelle anzulegen, in der für bestimmte Winkelmaße die entsprechenden Ticks bereits berechnet sind (Tabelle 1).
Bei einer Drehung um 90° gegen den Uhrzeigersinn lautet der entsprechende ActivityBot-Befehl
-
drive_goto(-26, 26)
3 - Polygonaler Pfad
Ein Polygon oder auch Vieleck besteht aus mindestens drei Punkten (nicht kollinear), die miteinander durch Strecken verbunden sind. Sie werden als Seiten oder Kanten bezeichnet, die Punkte auch als Ecken.
Bei drei Punkten ergibt sich ein Dreieck mit drei Seiten, bei vier ein Viereck mit vier Seiten und bei N Punkten (N aus der Menge der natürlichen Zahlen) ein N-Eck mit N Seiten. Haben alle Seiten die gleiche Länge, sprechen wir von einem regulären Polygon.
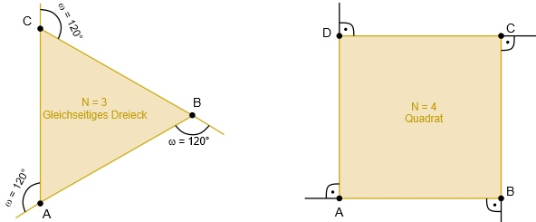
Einige Polygone sind in Abb. 2 dargestellt:
-
das Dreick (N = 3) -
das Viereck (N = 4) -
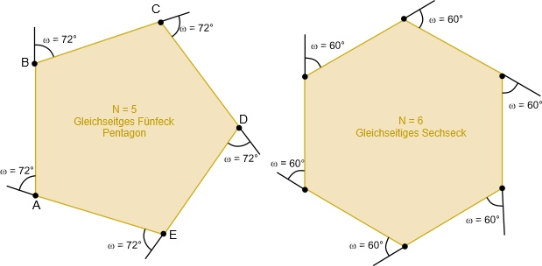
das Fünfeck (N = 5) -
das Sechseck (N = 6)
Von besonderem Interesse sind reguläre Polygone mit N >= 36; ihre Form nähert sich immer mehr einem Kreis an. Obwohl es keine echten Kreise sind (die haben keine Eckpunkte!), nähern sie sich ihnen sehr stark an, so dass wir sie genähert als Kreis ansehen.
Wir werden im folgenden Abschnitt den ActivityBot reguläre Polygone abfahren lassen.
4 - Roboter auf polygonalen Pfaden
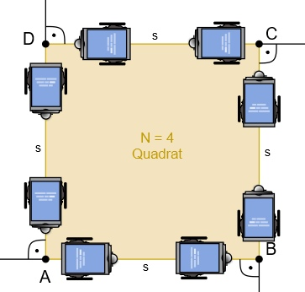
Man kann einen Roboter den Umriss eines Polygons nur dann genau abfahren lassen, wenn man die äußeren Winkelmaße (Ergänzungswinkel Omega zu 180°) von jedem Eckpunkt kennt. Für vier Polygone sind in den folgenden Abbildungen die Ergänzungswinkel angegeben. Er errechnet sich aus der Anzahl N der Ecken zu
Die Ergänzungswinkel zu jedem Eckpunkt und den regulären Polygonen Dreieck, Quadrat, 5-Eck und 6-Eck zeigen die folgenden Abbildungen.
5 - Reguläre Polygone mit dem ActivityBot abfahren
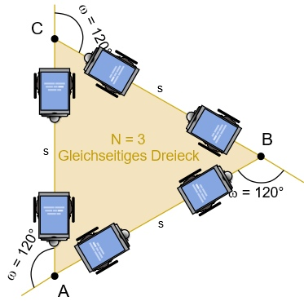
Um mit einem ActivityBot ein gleichseitiges Dreieck mit der Seitenlänge s abzufahren, müssen die folgenden Befehle gegeben werden
Ablauffolge der Befehle (freie Formulierung)
- Starte im Punkt A.
- Fahre eine Strecke s vorwärts.
- Drehe nach rechts um 120°
- Fahre eine Strecke s vorwärts.
- Drehe nach rechts um 120°.
- Fahre eine Strecke s vorwärts.
- Drehe nach rechts um 120°.
oder kürzer
Wiederhole dreimal
- Fahre eine Strecke s vorwärts.
- Drehe nach rechts um 120°.
| Mit dem ActivityBot ein gleichseitiges Dreieck abfahren | |
| Aufgaben |
|
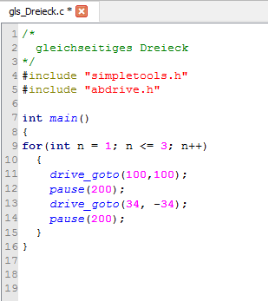
Das Programm gls_Dreieck.c
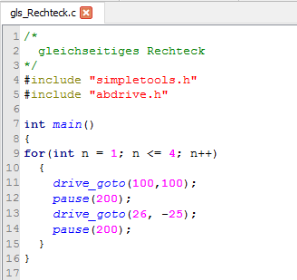
Die Ablauffolge der Befehle für ein gleichseitiges Rechteck mit der Seitenlänge s lautet in der Kurzfassung
| Mit dem ActivityBot ein gleichseitiges Rechteck abfahren | |
| Aufgaben |
|
Das Programm gls_Rechteck.c
- Schreibe jetzt selbst Programme für die Polygone mit N = 5 Ecken (Pentagon) und N = 6 Ecken (gleichseitiges Sechseck).
- Wie müsste ein Programm aussehen, dass den ActivityBot einen Halbkreis fahren lässt und anschließend wieder zum Ausgangspunkt zurückkehrt?
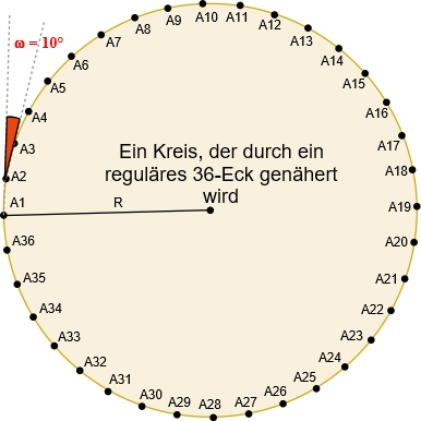
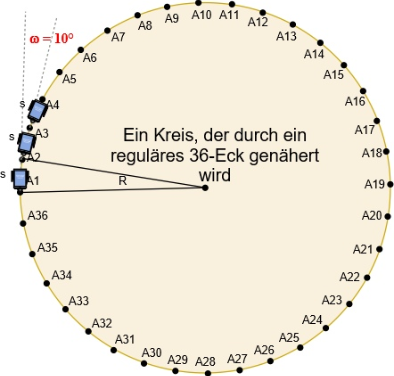
6 - Kreise mit regulären Polygonen nähern
Ein Kreis wird durch ein reguläres Polygon mit N >=36 angenähert. Im hier vorgestellten Beispiel wird N = 36 sein, damit entfällt auf jeden Polygonzug eine Drehung von 10°, insgesamt sind es dann 360°.
Um den ActivityBot auf eine Kreisbahn zu schicken, müssen die folgenden Befehle eingegeben werden
Die Größe von s bestimmt den Durchmesser des Kreises, den der Roboter nimmt. Du solltest deshalb einen kleinen Wert für s nehmen, vielleicht um die 8 Ticks.
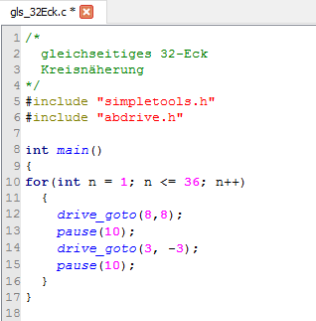
Das folgende SimpleIDE Programm für den ActivityBot lässt den Roboter einen Kreis von ca. 15cm Radius beschreiben.
| Mit dem ActivityBot ein gleichseitiges 32-Eck (einen Kreis) abfahren | |
| Aufgaben |
|
Das Programm gls_32Eck.c
7 - s in Abhängigkeit vom Kreisradius R berechnen
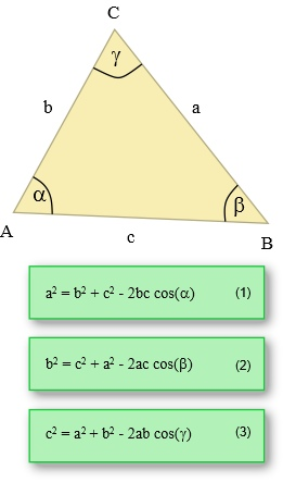
Welche Länge muss eigentlich die Strecke s haben, damit der Roboter einen Kreis vom Radius r fährt? Oder man kann auch direkt sagen: welcher mathematische Zusammenhang besteht zwischen der Strecke s und dem Kreisradius r? Gelöst wird diese Aufgabe mit dem Cosinussatz, der - je nachdem, welche der drei Seiten in einem beliebigen Dreieck gesucht ist, dies in je einer Formel darstellt.
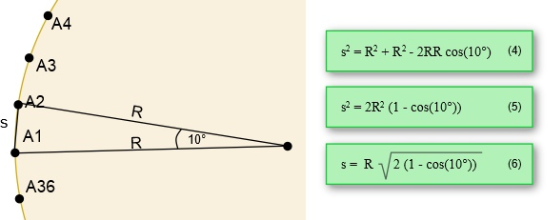
Angewendet auf das 32-Eck ergibt sich folgender Zusammenhang
Mit Hilfe dieser Formel ist es nun möglich ein Programm zu schreiben, dass einen Roboter einen Kreis mit einem bestimmten Radius R durchfahren lässt.
Wer tiefer graben möchte; weitere Informationen findet man auf der Seite von Parallax Inc.