Digitaltechnik - 0

1 - Logikgatter und Wahrheitstafeln

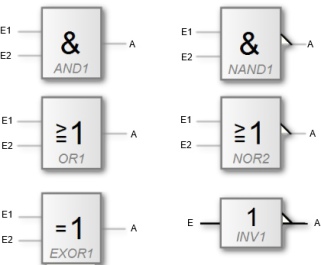
Logikgatter bilden die Grundfunktionen der sogenannten booleschen Algebra, die

AND-Funktion (Konjunktion)
OR-Funktion (Disjunktion)
NOT-Funktion (Negation)

auf elektronischem Weg mit Hilfe von elektronischen Gattern ab.

Im Gegensatz zur allgemeinen Schulalgebra mit rationalen und reellen Zahlen können die Eingangsgrößen der booleschen Algebra nur die Werte 1 (HIGH, LED AN) oder 0 (LOW, LED AUS) annehmen und die Ergebnisse der Verknüpfung zweier Eingangsgrößen nicht größer als 1 sein. Und es gibt weder bei der AND- noch bei der OR-Verknüpfung Überträge an höhere Binärstellen, so wie wir es im Dezimalsystem zum Beispiel bei der Addition gewohnt sind.

Zu den Grundfunktionen der booleschen Algebra ließen sich auch die beiden negierten Funktionen zu AND und OR zählen, die man kurz mit NAND (not AND) und NOR (not OR) abkürzt.

Wir werden uns hier mit den Grundfunktionen NAND, NOR, NOT und einer vierten Funktion EXOR (Exklusiv-ODER oder Antivalenz) beschäftigen, die sogenannten Wahrheitstabellen anschauen und einen Halb- und Volladdierer aus den insgesamt 6 Gattern aufbauen.

Als Hilfsmittel dient hier das Programm ProfiLab Expert bzw. ProfiLab der Fa. ABACOM.

Alternativ lassen sich die Wahrheitstafeln auch mit Hilfe eines Propeller Controllers P2 aufnehmen. Wie das geht, wird hier an Hand eines NAND-Gatters HD74LS00 exemplarisch gezeigt -> Übung 2.

2 - Schaltsymbole logischer Gatter

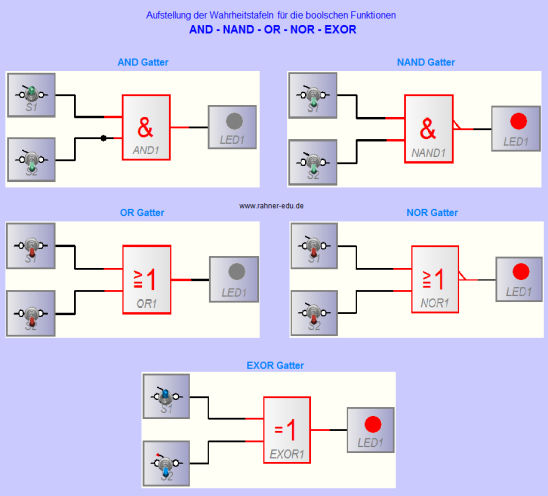
Abbildung 1 - Die in diesem Abschnitt verwendeten logischen Gatter und ihre Schaltsymbole

3 - Wahrheitstafeln erstellen

Zur Ermittlung der Wahrheitstafeln der logischen Funktionen kann das Programm ProfiLab Expert sehr gut eingesetzt werden. Für den Unterricht lassen sich die Schaltungen vorher kompilieren (.exe Datei) und den Schülern als ausführbare Datei zur Verfügung stellen. Eine mögliche Darstellung auf dem Bildschirm zeigt die folgende Abbildung:

Abbildung 2 - Die Datei logik-grundgatter.exe wird über Windows gestartet und ist sofort einsatzfähig. Die Schalter lassen sich umlegen und die LED am Ausgang zeigt das jeweilige Ergebnis an.

Wahrheitstabellen erstellen

Aufgaben

Starte die Datei logik-grundgatter.exe. Mit Hilfe der Schalter S lassen sich an die Eingänge HIGH (1) und LOW (0) Zustände legen.
Beginne mit dem AND-Gatter und lege mit Hilfe der beiden Schalter S1 und S2 an die Eingänge des Gatters nacheinander alle möglichen Kombinationen aus 0 und 1 (insgesamt 4). Notiere die zugehörigen Zustände der LED (leuchtet -> 1, leuchtet nicht -> 0) in einer Tabelle.
Verfahre bei allen fünf Gattern so, wie eben beschrieben.
Vergleiche deine Ergebnisse mit den hier dargestellten Ergebnissen.

Wahrheitstabellen

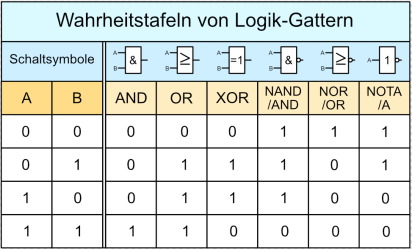
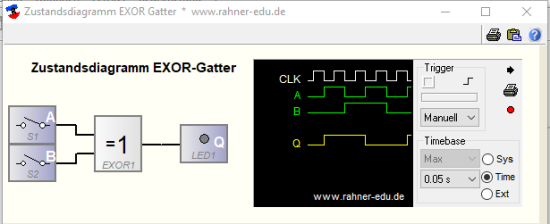
Abb. 1 - Logikgatter und ihre Wahrheitstabellen

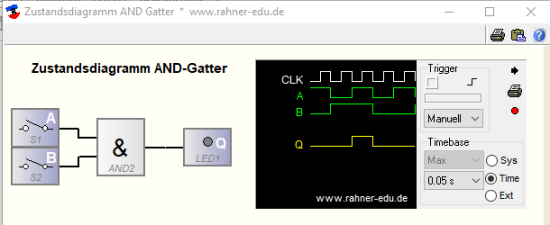
Die Spalten A und B in den Wahrheitstabellen stehen für die Eingänge des jeweiligen Gatters. Erfasst man die Eingangs- und Ausgangssignale mit einem eingangsseitigen Bitmustergenerator und ausgangsseitig mit einem Logikanalysator, lassen sich die Verknüpfungsglieder dynamisch untersuchen. Für zwei der oben genannten Grundgatter ergeben sich die folgenden Zustandsdiagramme:

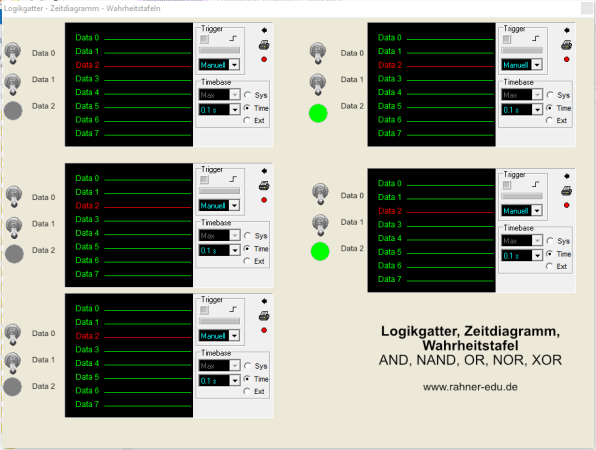
Abb. 2a - Zustandsdiagramm eines AND-Gatters. Ist A HIGH und B LOW, ist Q LOW, gleiches gilt für den umgekehrten Fall und wenn beide Eingänge LOW sind. Nur wenn beide Eingänge HIGH sind, ist auch der Ausgang HIGH.

Abb. 2b - Zustandsdiagramm eines EXOR-Gatters. Der Ausgang wird LOW, wenn A und B auf gleichem Pegel liegen, entweder beide LOW oder beide HIGH. Sind die Pegel an A und B ungleich, ist Q immer auf HIGH.

Teste dein Wissen - 1

Mit dem in Abb. 2c gezeigten Programm "Logikgatter_Zeitdiagramm.exe" kannst du dein Wissen über das Verhalten von Logikgattern noch einmal überprüfen. Entweder machst du das über die LED-Anzeige oder - was schwerer ist - über das Zeitdiagramm.

Abb. 2c - Ein Programm, in dem fünf Gatter "versteckt" sind. Über die Taster kann zu jedem Gatter der Ausgangspegel über eine LED oder ein Zeitdiagramm abgelesen werden. Finde heraus, welche Schaltung zu welchem Gatter gehört.

Wie arbeitet das Programm?

Abb. 2e

Erläuterungen zur Bedienoberfläche des Programms "Logikgatter-Zeitdiagramm.exe".

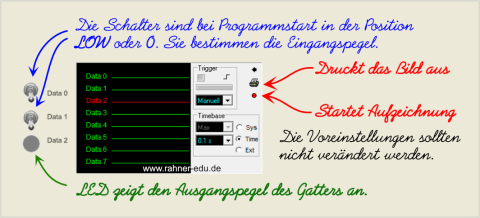
Nach dem Programmstart sucht man sich eine der fünf angebotenen Schaltungen aus. Über den roten Knopf wird die Aufzeichnung des Zeitdiagramms gestartet; dafür hast du ungefähr 10s Zeit.

1. Zähle "21, 22" und klicke anschließend auf den oberen Taster (Data 0).
2. Zähle "21, 22" und klicke auf den unteren Taster (Data 1).
3. Zähle "21, 22" und klicke auf den oberen Taster (Data 0).
4. Zähle "21, 22" und klicke auf den unteren Taster (Data 1).

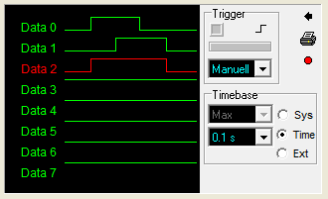
Wenn alle Tasterbewegungen ins Zeitfenster gepasst haben (vielleicht muss man es vorher ein-, zweimal üben), dann erhälst du z. B. folgendes Zeitdiagramm:

Abb. 2f - Aufgenommenes Zeitdiagramm für eines der unbekannten Logikgatter.

Teste dein Wissen - 2

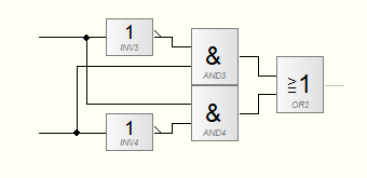
Analysiere die folgende Schaltung, indem du ihre Wahrheitstafel aufstellst. Wie lässt sich die Schaltung vereinfachen?

Abb. 2d - Wie verhält sich diese Schaltung und wie lässt sie sich vereinfachen? Stelle dazu eine Wahrheitstabelle auf.

4 - Addierschaltung

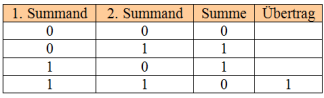
Schauen wir alle Möglichkeiten an, zwei Binärzahlen zu addieren.

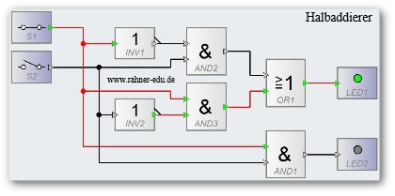
An der Summenspalte erkennt man, dass die Summe immer dann 1 ist, wenn einer der beiden Summanden 1 ist. Dies ist identisch mit der Wahrheitstafel eines EXOR-Gatters (Antivalenz). Kommt der Übertrag hinzu, dann muss für den Fall, dass beide Summanden 1 sind, eine 1 im Übertrag angezeigt werden. Die folgende Schaltung erfüllt die Wahrheitstafel.

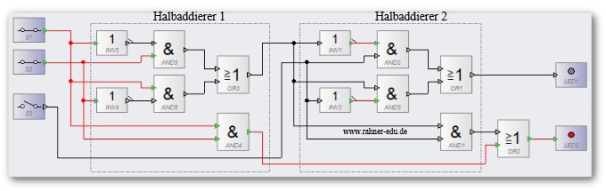
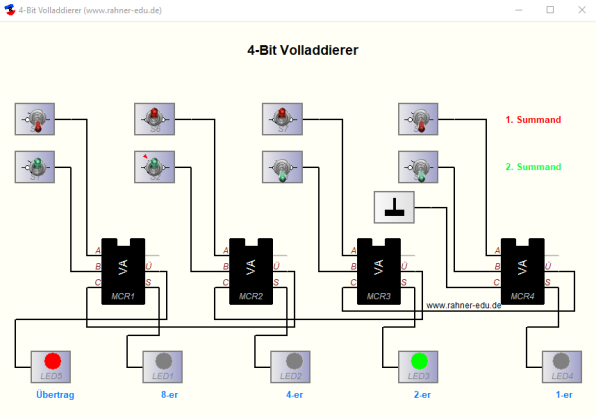
Abbildung 3 - Halbaddierer, aufgebaut aus AND- und OR-Gattern und Invertern. Dargestellt sind der Leitungszustand (rot) und der Bauteilzustand (grüne Dreiecke, LEDs, Taster). LED1 zeigt die Summe, LED2 den Übertrag an. Benutztes Programm: ProfiLab Expert

Der Halbaddierer ist in der Lage zwei Bits zu addieren; er zeigt einen Übertrag an, aber er kann keine Überträge, die von weiteren Additionsstufen kommen, verarbeiten. Aus diesem Grund ist es ein Halb- und kein Volladdierer. Erst durch das Hinzufügen eines dritten Eingangs, der einen Übertrag aus einer vorherigen Additionsstufe aufnimmt, wird der Halb- zum Volladdierer. Realisiert wird dies durch zwei hintereinandergeschaltete Halbaddierer wie in der folgenden Abbildung gezeigt.

Abbildung 4 - Volladdierer aus zwei Halbaddierern zusammengesetzt. Leitungs- und Bauteilzustand sind für den Fall 1 + 1 dargestellt. S3 ist der Übertragseingang, LED1 zeigt die Summe, LED2 den Übertrag an.

Fasst man die beiden Halbaddierer zu einem Makro zusammen, dann ergibt sich daraus ein Volladdierer (VA) mit 3 Eingängen (A, B, C) und zwei Ausgängen (S und Ü). Mit diesem VA-Baustein lässt sich dann ein 4-Bit Volladdierer aufbauen.

Abbildung 5 - 4-Bit Addierwerk aus vier Volladdierern. Mit dem Programm "4Bit-VA.exe" lassen sich binäre Additionen ausführen. Es dient zur Hinführung zu komplexeren Schaltungen und soll den Umgang mit dem Binärsystem üben.

5 - Rechenwerke

5.1 4-Bit Additions- / Subtraktionswerk

Etwas Theorie

Bisher lassen sich mit den vorgestellten Schaltungen nur binäre Zahlen addieren. In diesem Abschnitt stellen wir die Subtraktion binärer Zahlen und ein Additions-/ Subtraktionswerk vor.

Bei den meisten Rechenwerken wird eine Subtraktion auf eine Addition des Zweierkomplements des Subtrahenden zurückgeführt. Dieses Verfahren ist im dualen Zahlensystem besonders einfach. Betrachten wir dazu ein Beispiel.

Beispiel

Berechne die Differenz aus den beiden Zahlen 23 und 18: 23 - 18.

Die erste Zahl wird auch als Minuend, die zweite als Subtrahend bezeichnet. Es gilt immer: Minuend minus Subtrahend gleich Differenz.

Lösung

Stelle beide Zahlen zunächst im binären System dar.

Stellenwert	32	16	8	4	2	1
23	0	1	0	1	1	1
18	0	1	0	0	1	0

Es gilt: 23₁₀ (im Zehnersystem) entspricht die Zahl 10111₂ (im Binärsystem); entsprechend gilt für die Zahl 18₁₀ = 10010₂.

Bilde das Einerkomplement des Subtrahenden.
Dies ist gleichbedeutend damit, dass in der Binärdarstellung der Zahl alle Einsen zu Nullen und alle Nullen zu Einsen werden.

Dezimalzahl\Stellenwert	32	16	8	4	2	1	Aktion
23	0	1	0	1	1	1
/18	1	0	1	1	0	1	Einserkomplement von 18

Bilde das Zweierkomplement, d.h., addiere zum Einserkomplement der Zahl eine 1.

Dezimalzahl\Stellenwert	32	16	8	4	2	1	Aktion
23	0	1	0	1	1	1
/18 + 1	1	0	1	1	1	0	Zweierkomplement von 18

Addiere beide Zahlen

Dezimalzahl\Stellenwert	32	16	8	4	2	1	Aktion
23	0	1	0	1	1	1
/18 + 1	1	0	1	1	1	0	Zweierkomplement von 18
Ergebnis	1	0	0	1	0	1

Streiche die 1 im höchsten Bit des Ergebnisses; die restlichen Stellenwerte zeigen das Ergebnis der Subtraktion an:

010111 – 101110 = x00101

23 - 18 = 5

Der darstellbare Zahlenraum wird kleiner

Stehen uns nur vier Bit pro Operand zur Verfügung, heißt das, dass die niedrigste darstellbare negative Zahl -7 oder 1111 ist. Das höchstwertige Bit ist hier das Vorzeichenbit und verkleinert damit den darstellbaren Zahlenraum. Entsprechend ist die höchste darstellbare Zahl 0111₂ = 7₁₀.

Der Negativwert einer Zahl N entspricht ihrem Zweierkomplement /N +1.

5.2 Aufbau eines 4-Bit Additions-/ Subtraktionswerkes

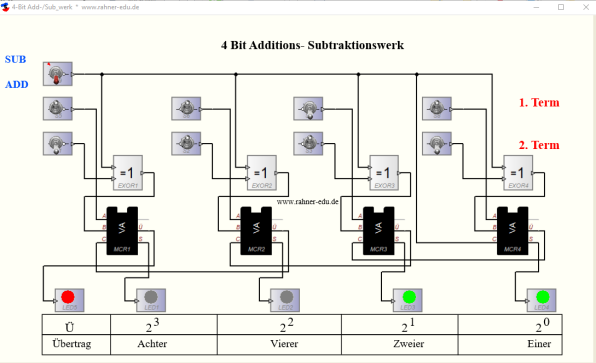
Eine Subtraktion wird über die Zweierkomplement-Bildung des Subtrahenden erreicht. Mit Hilfe von XOR-Gattern (siehe oben) wird die Negation (aus 1 wird 0 und aus 0 wird 1) umgesetzt. Dazu wird einer der beiden Eingänge des Gatters auf 1 gezogen bzw. der Schalter auf SUB gesetzt.

Abb. 6 – 4-Bit Additions- /Subtraktionswerk. Über den SUB/ADD Schalter wird eingestellt, ob eine Addition oder eine Subtraktion ausgeführt werden soll. Die vier Taster des 1. und 2. Terms werden entsprechend eingestellt; die LEDs zeigen durch Aufleuchten das Rechenergebnis an.

Legt man an den zweiten Eingang des XOR-Gatters das Subtrahenden-Bit (2. Term, siehe Abb. 6), wird es am Ausgang negiert, bei einer 0 nicht. Das Eingangsbit wird an den Ausgang unverändert weitergegeben.

Die Stellenwerte der LEDs sind bezeichnet. So lässt sich schneller das dargestellte Ergebnis in uns geläufigere Dezimalzahlen umrechnen.

zurück

6 - 8-Bit Additions-/Subtraktionswerk mit Steuerwerk

6.1 - 8-Bit Additionswerk

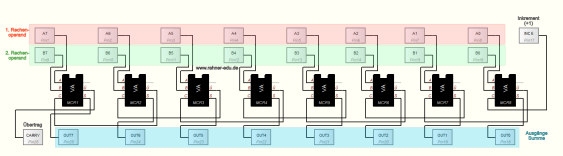
Wir haben gesehen, dass Rechenwerke mit 4-Bit Wortlänge sehr beschränkt und nicht gerade alltagstauglich sind. Deshalb werden wir im folgenden Abschnitt 6 ein 8-Bit Addierwerk und ein 8-Bit Additions-/ Subtraktionswerk mit Steuereinheit entwerfen. Die Basis bildet ein 8-Bit Additionswerk, das sich aus acht Volladdierern zusammensetzt, die in einem Makro "8-Bit-VA" abgelegt werden (s. Abb. 7).

Abb. 7 - 8-Bit Volladdierer. Er setzt sich zusammen aus zwei 8-Bit Tastatureingaben und einem Increment-Eingang (1. Rechenoperand, 2. Rechenoperand) sowie einer 8-Bit LED-Ausgabeeinheit mit Übertragsanzeige.

6.2 - Subtraktion zweier Binärzahlen

Aus vorher gemachten Überlegungen wissen wir, dass die Subtraktion zweier Binärzahlen auf eine Addition zurückgeführt wird.

A – B = A + (- B)

Eine negative Zahl lässt sich im binären Zahlenraum über das Zweierkomplement bilden. Dazu wird der Subtrahend B negiert (/B) und anschließend inkrementiert (+1).

-B = /B +1

Ein Beispiel

A = 1001₂ = 9₁₀ und B = 1100₂ = 12₁₀ seien gegeben.

Bestimme die Differenz der Zahlen:

B – A und
A – B.

1. Fall: A - B

Abb. 8

Bei der Differenzbildung wird wieder mit der Zweierkomplement-Arithmetik gearbeitet. Das höchste Bit im Ergebnis zeigt ein negatives Resultat an, wenn es 1 ist.

Das Zahlenergebnis einer negativen Zahl im Dualsystem wird durch eine einfache Umwandlung lesbar gemacht.

Abb. 9

Bei einem negativen Ergebnis muss die Darstellung zur besseren Lesbarkeit umgerechnet werden.

2. Fall: B - A

Vertauschen wir die beiden Operanden, dann wird das Ergebnis der Subtraktion aus

12 - 9 = 3

positiv ausfallen und in der binären Darstellung deutlich werden.

Abb. 9a

Die Subtraktion liefert ein positives Ergebnis. Nach Ausführung des Zweierkomplements weist das Ergebnis im MSB eine 0 aus. Das Ergebnis ist positiv.

Das MSB (most significant bit) im Differenzergebnis zeigt in der Zweierkomplement-Arithmetik das Vorzeichen an; dabei gilt:

0: die Differenz ist positiv

1: die Differenz ist negativ

Der 8-Bit Volladdierer aus Abb. 7 wird nun über ein Steuergerät so erweitert, dass Addition, Subtraktion, Zweierkomplementbildung und separat geschaltete Eingaben von Operanden möglich sind.

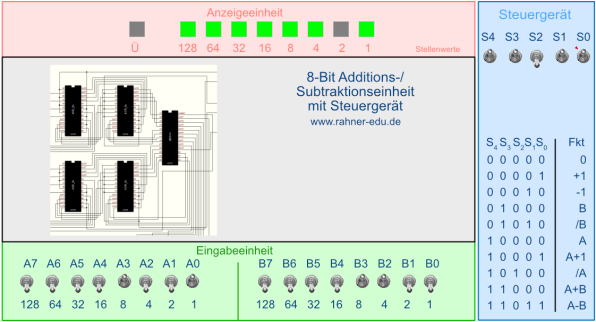
Abb. 10 - 8-Bit Additions-/ Subtraktionswerk mit Steuergerät

Die Oberfläche des Programms zeigen die folgenden Bilder:

Abb. 11

Programmoberfläche einer 8-Bit Additions-/Subtraktionseinheit mit Steuergerät

In der Eingabeeinheit sind die beiden Zahlen 1001₂ und 1100₂ aus dem obigen Beispiel eingestellt. Es wird berechnet:

1001₂ - 1100₂.

Im Steuergerät wurde die Bitfolge 11011₂ eingestellt, die für eine Subtraktion steht. Das Ergebnis zeigt die Anzeigeeinheit. Das MSB ist HIGH, damit ist das Ergebnis NEGATIV.

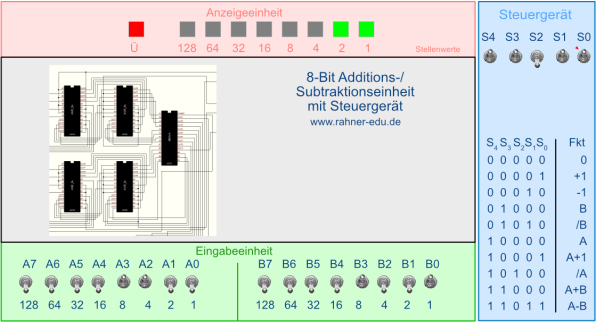
Abb. 12

Programmoberfläche einer 8-Bit Additions-/Subtraktionseinheit mit Steuergerät

In der Eingabeeinheit sind die beiden Zahlen 1001₂ und 1100₂ aus dem obigen Beispiel eingestellt. Es wird berechnet: 1100₂ - 1001₂.

Im Steuergerät wurde die Bitfolge 11011₂ eingestellt, die für eine Subtraktion steht. Das Ergebnis zeigt die Anzeigeeinheit. Das MSB ist LOW, damit ist das Ergebnis positiv und wie angezeigt: 3₁₀.

6.3 - Rechenoperationen mit der 8-Bit Additions-/Subtraktionseinheit mit Steuerwerk

S4	S3	S2	S1	S0	Bedeutung	Bemerkungen
0	0	0	0	0	0	Die Eingabeeinheit ist gesperrt, es werden keine Daten an die Anzeigeeinheit übertragen. Alle LEDs sind ausgeschaltet: 0000 0000.
0	0	0	0	1	+1	Zum angezeigten Wert in der Anzeigeeinheit wird 1 addiert.
0	0	0	1	0	-1 oder 255	Alle acht LEDs sind auf HIGH.
0	1	0	0	0	B	Die über die Schalter B0 ... B7 der Eingabeeinheit eingestellten Binärwerte werden an die Anzeigeeinheit übergeben.
0	1	0	1	0	/B = -B - 1	Einerkomplement von B
1	0	0	0	0	A	Die über die Schalter A0 ... A7 der Eingabeeinheit eingestellten Binärwerte werden an die Anzeigeeinheit übergeben.
1	0	0	0	1	A + 1	Der Wert von A wird um 1 erhöht.
1	0	0	1	0	A - 1	Der Wert von A wird um 1 erniedrigt. Das Übertragsbit geht auf HIGH.
1	0	1	0	0	/A = -A - 1	Einerkomplement von A
1	1	0	0	0	A + B	Summe von A und B.
1	1	0	1	1	A - B	Differenz von A und B. Ist Bit 8 in der Anzeigeeinheit 0, ist das Ergebnis positiv, ist es 1, negativ. Eine negative Binärzahldarstellung kann über: (Zweierkomplementbildung des Ergebnisses) + 1 in eine lesbarere Form gebracht werden.
1	1	1	0	1	B - A	Differenz von B und A. Ist Bit 8 in der Anzeigeeinheit 0, ist das Ergebnis positiv, ist es 1, negativ. Eine negative Binärzahldarstellung kann über: (Zweierkomplementbildung des Ergebnisses) + 1 in eine lesbarere Form gebracht werden.

Tabelle 1 - Eine Auswahl aufrufbarer Funktionen der 8-Bit Additions-/Subtraktionseinheit mit Steuerwerk (s. Abb. 12).

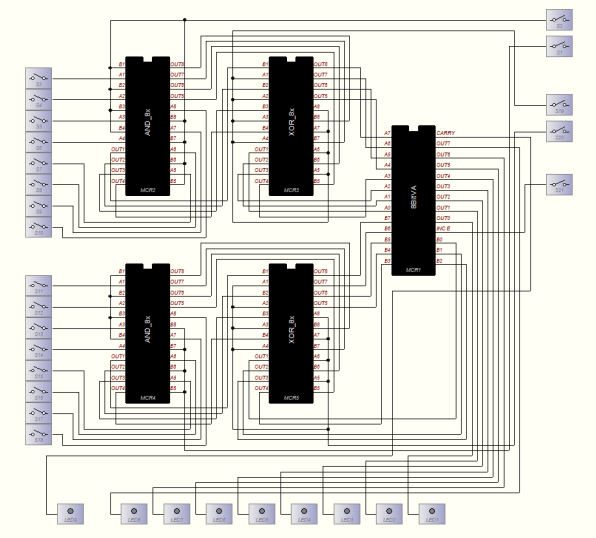
In einem weiteren Schritt wird das 8-Bit Additions-/ Subtraktionswerk mit Steuergerät als Makro abgespeichert und zu einer arithmetisch-logischen Einheit oder ALU erweitert. Es kommen die drei logischen Verknüpfungen XOR, AND und OR sowie ein Datenselektor mit vier Steuersignale hinzu.

Schaltungen, die dies vermögen, werden arithmetic logical units, kurz: ALU, genannt.

Wie eine solche ALU aufgebaut ist und arbeitet, werden wir uns im folgenden Kapitel anschauen. Auch hier bedienen wir uns des Programms ProfiLab.

Wenn dich das Kapitel "Arithmetisch-Logische-Einheit oder ALU" interessiert, geht es hier weiter.

zurück