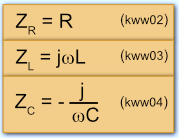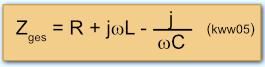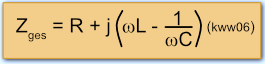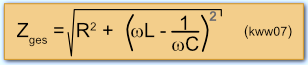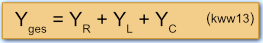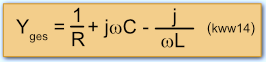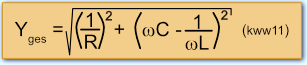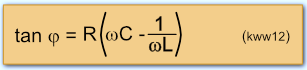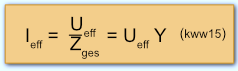Schwingkreise
Wir unterscheiden zwischen einem
- Serienresonanzkreis oder Reihenresonanz- oder kurz Reihenschwingkreis und
- Parallelresonanzkreis oder Parallelschwingkreis
Im ersten Fall sind die Bauelemente R, L und C in Reihe, im zweiten Fall parallel angeordnet.
Der Frequenzgang (frequency response) eines RLC-Schwingkreises zeigt sich in seiner Verhaltensänderung bei unterschiedlichen Signalfrequenzen.
Resonanz liegt in einem RLC-Schaltkreis vor, wenn kapazitiver und induktiver Blindwiderstand (Reaktanz) gleich groß sind. Es liegt in diesem Fall eine rein ohmsche Impedanz (Wirkwiderstand) vor.
Begrifflichkeiten, die bekannt sein sollten:
- Blindwiderstand
- Impedanz, Scheinwiderstand oder komplexer Widerstand Z
- Wirkwiderstand R
- Widerstandszeiger in der komplexen Ebene.
Der Reihenschwingkreis
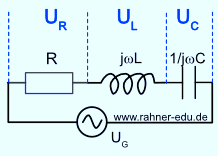
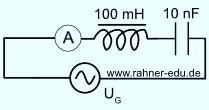
Ein Serienresonanzkreis oder Reihenschwingkreis besteht aus den drei Elementen: ohmscher Widerstand R, Kapazität C und Induktivität L, die in Reihe angeordnet sind und von einer sinusförmigen Wechselspannungsquelle versorgt werden.
Der Kondensator benötigt in periodischen Zeitabständen Energie zum Aufbau eines elektrischen Feldes zwischen seinen Platten und die Spule zum Aufbau eines magnetischen Feldes. Die in den Feldern gespeicherte Energie wird - ebenfalls in periodischen Zeitabständen - durch den Abbau der Felder wieder freigesetzt.
Im Idealfall - ohne ohmsche Wärmeverluste - könnte dieser Vorgang ohne weitere Energiezugabe, wenn einmal angestoßen, permanent ablaufen. Die Energie des elektrischen Feldes eines geladenen Kondensators wird zum Aufbau des magnetischen Feldes der Spule genutzt und umgekehrt; die Energie pendelt quasi zwischen beiden Bauteilen periodisch hin und her. Leider sieht die Praxis etwas komplexer aus und Schuld daran sind die ohmschen Verluste innerhalb der Schaltung in Form von Wärme. Der einmal angestoßene Energieaustausch zwischen Spule und Kondensator wird gedämpft und statt einer ungedämpften entsteht "nur" eine gedämpfte Schwingung.
Theorieteil zum Serienschwingkreis
Am Reihenschwingkreis aus R, L und C soll eine sinusförmige Wechselspannung Ueff anliegen. Dann gilt für den komplexen Wechselstromwiderstand Z der Schaltung:
mit
Das negative Vorzeichen in Formel kww04 deutet an, dass die Spannung dem Strom um 90° hinterher hinkt. Einsetzen der Größen aus kww02 - kww04 ergibt für den gesamten Scheinwiderstand der Schaltung:
oder mit Ausklammern des j-Termes:
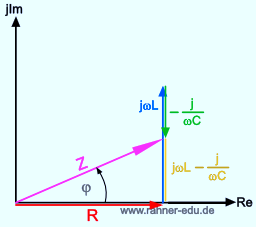
Das Zeigerdiagramm des Reihenschwingkreises hat dann die folgende Darstellung:
Der Winkel Phi gibt die Phasenverschiebung zwischen Strom und Spannungsgröße an. Der Betrag des gesamten Wechselstromwiderstandes (Scheinwiderstand, Impedanz) errechnet sich über:
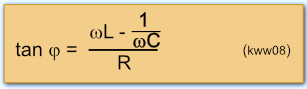
wobei für die Phasenverschiebung zwischen Strom- und Spannungsgröße aus dem Zeigerdiagramm folgt:
Resonanzfrequenz
Der Blindwiderstand aus Spule und Kondensator ist nach kww03 und kww04 frequenzabhängig. Bei einer bestimmten Frequenz f0 heben sich Xc und XL gegenseitig auf und der Blindwiderstand wird Null. Für diesen Fall gilt:
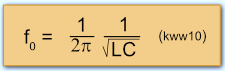
Auflösen der Gleichung nach der Frequenz f ergibt:
Gibt man die Induktivität in Henry (H), die Kapazität in Farad (F) an, ergibt sich die Frequenz in Hertz (Hz). f0 bezeichnet man als Resonanzfrequenz des Reihenschwingkreises. Die Phasendifferenz ist an dieser Stelle nach kww08 Null und der Scheinwiderstand Z = R nach kww07. Formel kww10 wird auch als Thomsonsche Schwingungsformel bezeichnet.
Für einen Serien-Resonanzkreis gilt:
- Im Resonanzfall ist nur der Wirkwiderstand wirksam; Strom und Spannung sind in Phase. Der kapazitive und induktive Widerstand heben sich in ihrer Wirkung gegenseitig auf.
- Bei Serienresonanz ist die Stromstärke im Kreis maximal und die Impedanz minimal.
- f < f0 - Schwingkreis verhält sich kapazitiv.
- f > f0 - Schwingkreis verhält sich induktiv.
- f = f0 - Schwingkreis verhält sich ohmsch.
- Aus kww10 folgt, dass die Resonanzfrequenz f0 um so geringer ist, je größer das Produkt aus L und C ist.
Übung 1 - Bestimmung der Resonanzfrequenz
| Resonanzfrequenz beim Reihenschwingkreis | |
| Material |
|
| Aufgaben |
|
Schaltskizze
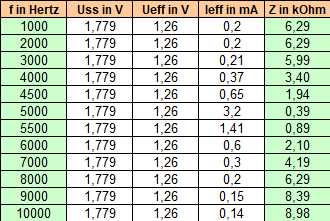
Messergebnisse
Graphische Auswertung
Rechnerische Bestimmung der Resonanzfrequenz
Nach Formel kww10 ergibt sich mit den Werten L = 0,100 H, C = 10 nF für die Grenzfrequenz
- f0 = 5033 Ohm.
Graphische Ermittlung der Resonanzfrequenz und des Wirkwiderstandes
Die Ausschnittvergrößerung zeigt, dass die Grenzfrequenz bei ungefähr
- f0 = 5050 Hz
liegt und der Wirkwiderstand der Gesamtschaltung bei ungefähr
- R = 250 Ohm.
Der vom Spulenhersteller angegebene Wert für den ohmschen Widerstand liegt bei R = 155 Ohm.
Der Parallelschwingkreis
Theorieteil zum Parallelschwingkreis
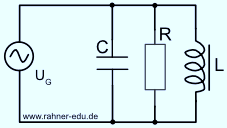
Am Parallelschwingkreis aus R, L und C soll eine sinusförmige Wechselspannung Ueff anliegen. Dann gilt für den komplexen Wechselstromleitwert Y der Schaltung:
Setzt man die entsprechenden Leitwerte in kww13 ein, erhält man:
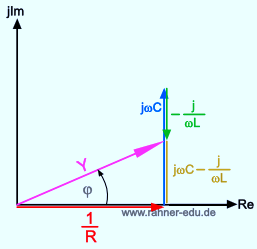
Die Phasenverschiebung erscheint im Zeigerdiagramm als Winkel zwischen der reellen Achse und dem Gesamtleitwert Y.
Der Betrag des Gesamtleitwertes ergibt sich aus dem Zeigerdiagramm zu:
und die Phasenverschiebung zu:
Wie beim Reihenschwingkreis ergibt sich für einen Parallelschwingkreis für die Resonanzfrequenz die Formel kww10. Wer die Formel herleiten möchte: im Resonanzfall gilt, dass der Blindleitwert Null werden muss. Löst man die Gleichung dann nach der Frequenz f auf, erhält man kww10.
Übung 2 - Bestimmung der Resonanzfrequenz
| Bestimmung der Resonanzfrequenz eines Parallelschwingkreises | |
| Material |
|
| Aufgaben |
|
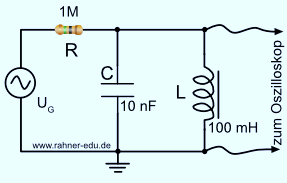
Schaltskizze
Der ohmsche Widerstand R = 1 MOhm begrenzt den Stromfluss in der CL-Schaltung nach
je nach angelegter Generatorspannung UG auf wenige µA.
Daraus ergibt sich auch, dass bei fehlendem Widerstand R und niedrigen Frequenzen die Stromleitung fast nur über die Spule und bei hohen Frequenzen über den Kondensator erfolgt.
Bei der Resonanzfrequenz fließt in der Hauptleitung kein Strom.
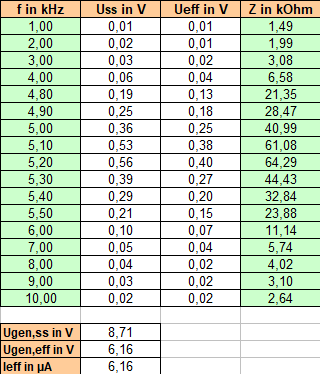
Messergebnisse
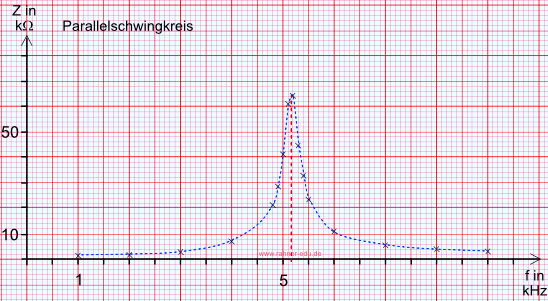
Graphische Auswertung
Rechnerisch liegt die Resonanzfrequenz bei 5033 Hz(siehe Übung 1). Experimentell ergibt sich ein Wert von ca. 5080 Hz.
Über ein 2-Kanal-USB-Oszilloskop lässt sich sehr gut zeigen (Lissajous-Figur), dass die Phasenverschiebung für niedrige Frequenzen f << f0 bei -Pi/2 liegt und für f >> f0 bei +Pi/2. Bei der Resonanzfrequenz tritt ein Phasensprung von Pi auf.