SPIN2 - Debug SCOPE
1. Trigonometrische Funktionen und Winkelmaße (Theorieteil)
Winkelmaße lassen sich in SPIN2 sowohl in Grad als auch im Bogenmaß verarbeiten. Bei Gradmaßen umfasst die Periode 360°, beim Bogenmaß entsprechend 2Pi.
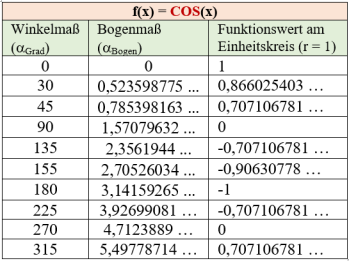
Für die klassischen trigonometrischen Funktionen sin(x) und cos(x) gelten damit folgende Beziehungen, die sich leicht mit einem Taschenrechner nachprüfen lassen:
Abb. 1a
Einige Tabellenwerte zur cos-Funktion für Winkel- und Bogenmaß.
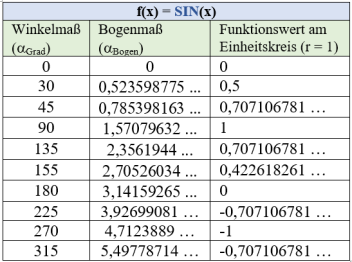
Eine gleiche Tabelle kann für die sin-Funktion erstellt werden:
Abb. 1b
Einige Tabellenwerte zur sin-Funktion für Winkel- und Bogenmaß.
Wie diese Winkelmaße vom Propeller2 bzw. in SPIN2 mit einer Ganzzahlarithmetik verarbeitet werden kann, zeigt Übung 1. Abb. 1a und b dienen zum späteren Vergleich mit den rechnerisch ermittelten Werten des Propeller P2 in der folgenden Übung.
Vorher müssen wir uns aber noch etwas mit Polarkoordinaten und deren Umrechnung in kartesische Koordinaten im 2-dim Raum kümmern.
2. Polarkoordinaten - kartesische Koordinaten
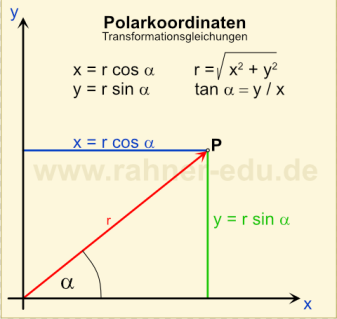
Einen beliebigen Punkt P in einer 2-dim Ebene kann man durch einen Ortsvektor r darstellen (s. Abb. 2). In kartesischen Koordinaten ist er durch die Angabe der x- und y-Koordinate von r eindeutig bestimmt.
Polarkoordinaten liegen dann vor, wenn ein Punkt P durch die beiden Angaben:
- Länge r vom Ursprung zum Punkt P und
- Winkel alpha mit der x-Achse
bestimmt ist.
Die Koordinaten beider Systeme lassen sich durch sogenannte Transformationsgleichungen ineinander überführen (s. Abb. 2).
Abb. 2
Transformationsgleichungen zur Umrechnung von Polarkoordinaten in kartesische Koordinaten und umgekehrt.
Da der Propeller P2 von Haus aus über eine Ganzzahlarithmetik verfügt, müssen weitere Dinge bei der Umrechnung beachtet werden, die in der folgenden Übung angegangen werden.
Übung 1 - Polarkoordinaten in kartesische Koordinaten umrechnen
| Übung 1 - Polarkoordinaten - kartesische Koordinaten | |
| Material |
|
| Aufgaben |
|
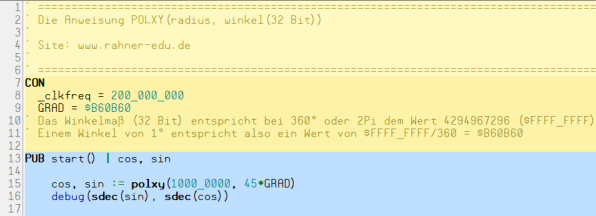
Das Programm Winkel.spin2
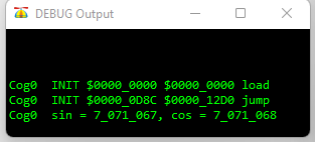
Die Ausgabe im Debug-Fenster
Abb. 3
Angezeigt wird der Sinus- bzw. Cosinus-Wert bei einem Winkel von 45°. Durch die Ganzzahlarithmetik werden nur die Ziffernfolgen angezeigt.
Wie arbeitet das Programm Winkel.spin2 ?
Insgesamt besteht das Programm nur aus zwei Konstantendeklarationen und zwei Anweisungsschritten.
Für die debug-Anweisungen muss die Taktfrequenz bei mindestens 10 MHz liegen. Mit
- _clkfreq = 200_000_000
Wurde sie hier auf 200 MHz eingestellt. Die zweite Konstante ist
- GRAD = $B60B60
Dieser Wert ergibt sich aus dem Hinweis in Programmzeile 10 und 11. Es verbleibt nur das Hauptprogramm start() mit den beiden lokalen Variablen cos und sin.
Die Anweisung
- polxy(Länge, Winkel)
benötigt die Polarkoordinaten Länge und Winkel eines Punktes P, rechnet sie in cartesische Koordinaten um und gibt beide Werte in einer Programmzeile aus (Programmzeile 15).
Über die nachfolgende debug-Anweisung werden die errechneten Werte im Debug Output-Fenster angezeigt.
Die Länge wurde in Zeile 15 mit 10_000_000 angegeben. Aus diesem Grund muss man den errechneten und angezeigten sin- bzw. cos-Wert durch diesen Wert teilen, um den Fließkommawert zu erhalten. Das wäre in diesem Fall: 0,7071068.
Erhöht man den Längenwert um eine weitere Zehnerpotenz, wird das Ergebnis um eine Stelle erweitert. Angezeigt wird: 0,70710681.
Mit diesen Informationen kann jetzt die grafische Darstellung der beiden trigonometrischen Funktionen sin und cos mit Hilfe der Anweisung DEBUG SCORE durchgeführt werden.
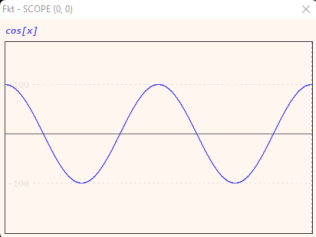
Übung 2 - Graph der Funktion cos(x)
Zur graphischen Darstellung von Daten steht unter DEBUG u.a. die Instruktion SCOPE bereit.
Mit folgenden Instruktionen im Bereich
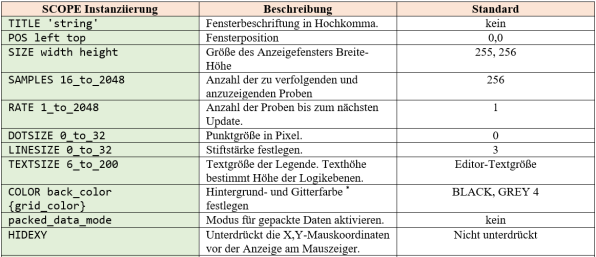
- SCOPE - Instanziierung (s. Abb. 4a) und
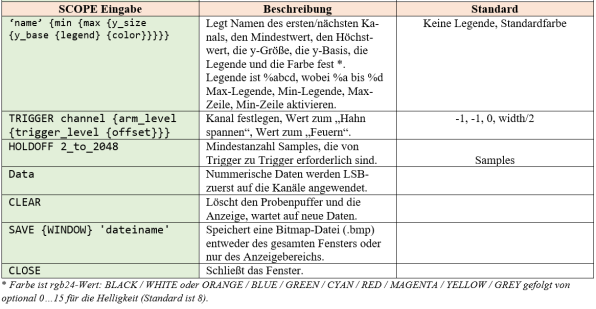
- SCOPE - Eingabe (feeding) (s. Abb. 4b).
Diese Informationen wurden entnommen aus Parallax Spin 2 Documentation v35s (Parallax Inc.).
a - DEBUG-SCOPE - Instanziierung
Abb. 4a - Instruktionen zur SCOPE Instanziierung
b - DEBUG-SCOPE - Eingabe (feeding)
Abb. 4b - SCOPE Eingabe Instruktionen (feeding)
In der folgenden Übung geht es darum, die trigonometrische Funktion COS am Einheitskreis graphisch darzutellen.
| Übung 2 - Graphische Darstellung der COS-Funktion am Einheitskreis | |
| Material |
|
| Aufgaben |
|
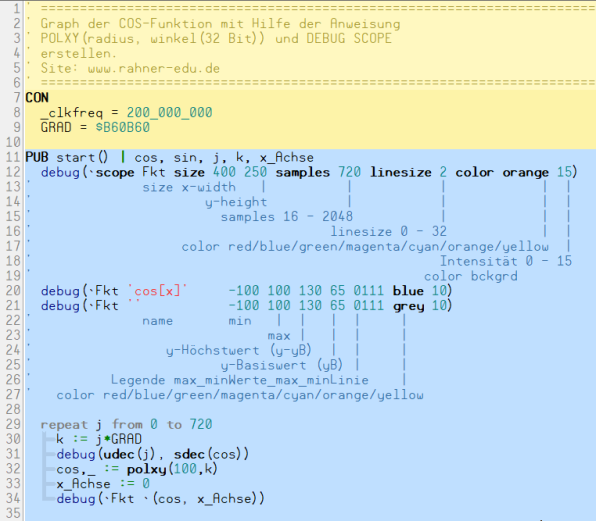
Das Programm cos-funktion.spin2
Abb. 5a - Graph einer cos-Funktion am Einheitskreis mit Hilfe von DEBUG-SCORE erstellen. Die Bedeutung der Parameter zu den einzelnen Instruktionen ist den Kommentarzeilen zu entnehmen.
Die graphische Darstellung unter DEBUG SCOPE
Abb. 5b
Graphische Darstellung der cos-Funktion am Einheitskreis mit Hilfe von DEBUG-SCOPE.
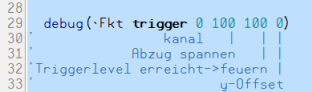
- Füge als nächstes zwischen Programmzeile 28 und 29 die neue Programmzeile 29 aus Abb. 6 ein und starte das Programm neu. Wie wird jetzt die Graphik aufgebaut?
Abb. 6
Das Programm aus Abb. 5a wird vor der repeat-Schleife ergänzt um die Programmzeile 29 in dieser Abbildung.
Zwischen Programmzeile 20 und 21 (s. Abb. 5) füge eine neue Zeile ein mit
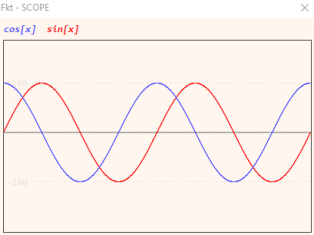
- debug(`Fkt 'sin[x]' -100 100 130 65 0111 red 8)
und ergänze in Zeile 35 den debug-Befehl:
- debug(`Fkt `(cos, sin, x_Achse)).
Starte das Programm neu. Es sollten die beiden Funktionen sin und cos erscheinen.
Abb. 7
Darstellung der Funktionen sin und cos am Einheitskreis mit Hilfe von DEBUG-SCOPE.
Druckversion 