Digitaltechnik – 2
0 - Beschreibung logischer Zusammenhänge mit Hilfe der booleschen Algebra
Beim Entwurf digitaler Schaltungen steht man häufig vor der Aufgabe, aus einer vorgegebenen Wahrheitstafel eine möglichst einfache boolsche Gleichung zu entwickeln. Für das Formulieren eines der Tafel entsprechenden booleschen Ausdrucks gibt es die Verfahren der disjunktiven und konjunktiven Normalform, während das Auffinden der einfachsten Form (Minimierung) erheblich schwieriger ist. Dafür wenden wir hier die Methode nach Karnaugh und Veitch (KV) an. Dabei werden die Variablen in sog. KV-Tafeln dargestellt.
1 - Die disjunktive Normalform (DNF)
Wie entsteht aus einer Wahrheitstafel nun ein boolescher Term, der die Verknüpfungen beschreibt? Es gibt zwei verschiedene Ansätze: die disjunktive und die konjunktive Normalform. Ich werde hier nur die disjunktive Normalform (DNF) beschreiben.
Disjunktive Normalform
In der disjunktiven Normalform werden alle Konjunktionen (AND-Funktionen) der Eingangsvariablen A, B, C, … disjunktiv (mit OR) verknüpft, die den Wert 1 oder HIGH haben.
Beispiel 1
|
A |
B |
C |
Q |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
Tabelle 1 - Wahrheitstafel einer logischen
Verknüpfung mit den drei Eingangsvariablen
A, B und C und der Ausgangsgröße Q.
Die DNF lässt sich wie folgt aus der Wahrheitstafel (s. Tabelle 1) ableiten:
- Markiere alle Zeilen in der Spalte Q, die eine 1 enthalten (hier rot markiert).
- Stelle für jede markierte Zeile einen booleschen Produktterm auf. Dort wo eine 1 steht, schreibe den Spaltennamen auf, dort wo eine 0 steht setze hinter den Spaltennamen ein Apostroph (Negation).
- Stelle die disjunktive Normalform her, indem du alle Minterme addierst.
- Q = A´B´C´ + A´B´C + A´BC + AB´C´
- Vereinfache den Term mit Hilfe boolescher Regeln.
Q = B´C´ + A´C (DNF)
2 - KV-Tafel
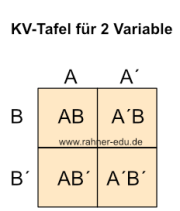
Die KV-Tafel für zwei Variable enthält je eine Spalte für die Variable A und ihr Komplement A´, sowie je eine Zeile für die Variable B und ihr Kompliment B´.
Dort, wo in einer Funktionstabelle in der Ausgangsspalte eine 1 steht, werden die zugehörigen Eingangsgrößen, die ebenfalls eine 1 ausweisen mit ihrem Bezeichnernamen (z. B. A, B o.ä. ) aufgeschrieben und die, bei denen eine 0 steht, erhalten zusätzlich zum Bezeichnernamen ein Apostroph (z. B. A´, B´ o.ä.). Minterme sind immer AND-Verknüpfungen (Multiplikation).
Nachbarschaftsregel für KV2
Benachbarte Felder dürfen zusammengefasst werden.
2.1 - Übungsbeispiele zu KV2
Nach der Nachbarschaftsregel für KV2 gilt:
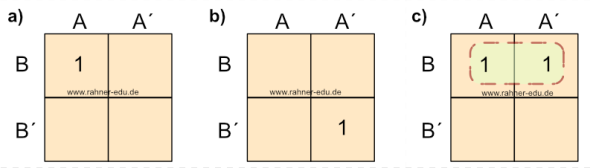
- Q = A * B = AB (Abb. 2a)
Entsprechend gilt für Abb. 2b die Gleichung
- Q = A´ * B´ = A´ B´ (Abb. 2b)
Der Malpunkt kann - wie in der klassischen Algebra auch - weggelassen werden, wenn es nicht zu Unstimmigkeiten kommt.
Die weiteren Beispiele ergeben die booleschen Gleichungen:
- Q = B (Abb. 2c)
Die weiteren Beispiele ergeben die booleschen Gleichungen:
- Q = A´ (Abb. 2d)
- Q = B + A´ (Abb. 2e)
- Q = A´ B + A B´ (Abb. 2f)
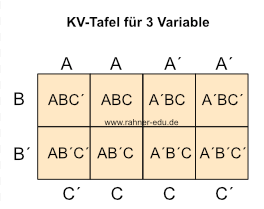
Die KV-Tafel für drei Variable besteht aus vier Spalten und zwei Zeilen.
Nachbarschaftsregel für KV3
Als benachbart gelten auch solche Felder, die an gegenüberliegenden Enden derselben Zeile liegen. Die Anzahl der jeweils in einer Gruppe zusammengefassten Felder muss eine Potenz von 2 sein.
2.2 - Übungsbeispiele zu KV3
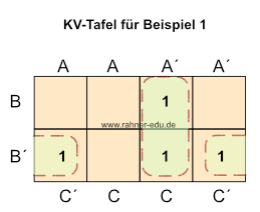
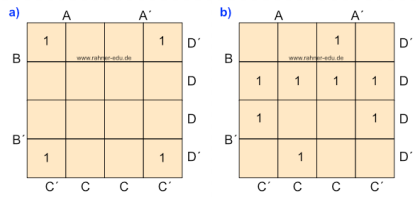
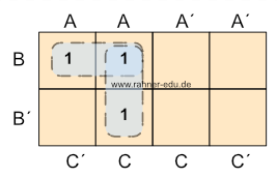
Die Gleichung aus Zeile 4 im Beispiel 1 wird in eine KV-Tafel für drei Variable übertragen, indem man alle Terme entfernt, die nicht in der Gleichung vorkommen und für die vorkommenden Terme eine 1 schreibt. Die KV-Tabelle hat dann das folgende Aussehen:
Als Ergebnisterm erhält man nach der Nachbarschaftsregel für KV3 für die Wahrheitstafel aus Beispiel 1 in diesem Kapitel:
- A´C + B´C´
was zu erwarten war, da dieses Ergebnis schon über die DNF in Übung 1 bestimmt wurde.
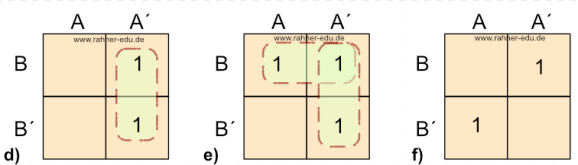
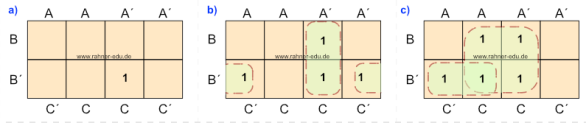
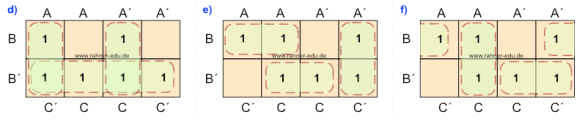
Aus den folgenden Bildern der Abbildung 5 können die folgenden Funktionen abgelesen werden (bitte unbedingt selbst nachvollziehen!!!):
- A´ B´ C (Abb. 5a)
- A´ C + B´ C´ (Abb. 5b)
- C + A B´ (Abb. 5c)
- A C´+ A´ C + B´ (Abb. 5d)
- A B + B´ C + A´ C´ (Abb. 5e)
- A C + A´ B´ + B C´ (Abb. 5f)
Wie man erkennt, ist die Verteilung und Anzahl der Einsen in Abb. 5e und 5f identisch, führen aber zu unterschiedlichen aber gleichwertigen Funktionsgleichungen. Es müssen so viele Gruppen gebildet werden, dass jede 1 erfasst ist.
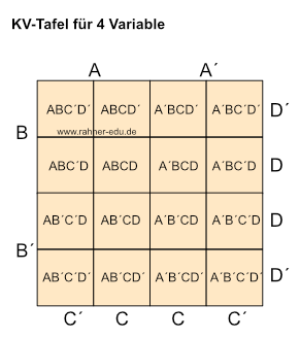
Die KV-Tafel für vierVariable besteht aus vier Spalten und vier Zeilen. Die Nachbarschaftsregel muss jetzt abgeändert werden.
Nachbarschaftsregel für KV4
Als benachbart gelten sowohl Felder, die an gegenüberliegenden Enden derselben Zeile liegen, als auch solche, die an gegenüberliegenden Enden derselben Spalte liegen.
2.3 - Übungsbeispiele zu KV4
Aus den Bildern der Abbildung 7 können die folgenden Funktionen abgelesen werden (bitte unbedingt selbst nachvollziehen!!!):
- C´ D´ (Abb. 7a)
- BD + A´ B C + C´ D + A B´ C D´ (Abb. 7b)
2.4 - Don´t Care Positionen
In der Praxis findet man häufig Schaltungen, bei denen bestimmte Kombinationen der Eingangsvariablen nicht auftreten. Wenn das der Fall ist, ist es völlig gleichgültig, wie sich eine Schaltung dann in solchen Fällen verhalten würde. Als Beispiel sei die folgende Tabelle genommen.
|
A |
B |
C |
Q |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
X |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
X |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
Tabelle 2 – Wahrheitstabelle mit frei wählbaren Ausdrücken (don´t care positions)
Die Ausgangsvariable Q ist an den beiden mit einem X gekennzeichneten Stellen frei wählbar und die zugehörigen Eingangskombinationen heißen „frei wählbare Ausdrücke“ oder „don´t care positions“. Man spricht auch von einer redundanten logischen Verknüpfung.
Don´t cares können in redundanten logischen Verknüpfungen zur Vereinfachung logischer Ausdrücke in KV-Tafeln verwendet werden. Dazu werden die Kreuze zusätzlich zu den Einsen eingetragen und können zum Bilden von Gruppen herangezogen oder auch nicht berücksichtigt werden.
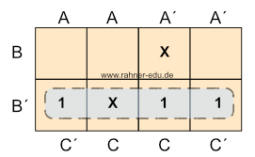
Aus dem Beispiel in Abb. 8 liest man den Ausdruck ab:
- Q = B´
3 - Übung zur DNF und KV-Diagramm
Beim Entwurf digitaler Schaltungen arbeitet man mit Funktionstabellen, Mintermen und KV-Diagrammen. An einer Beispielschaltung, deren Funktionstabelle vorliegt, wird gezeigt, wie die Minterme aufgestellt, das KV-Diagramm erzeugt und die Minimierung darüber erfolgt.
|
Eingänge A B C |
Ausgang Q |
Minterm
|
| 0 0 0 | 0 | |
| 0 0 1 | 1 | A´ B´ C |
|
0 1 0 |
1 | A´ B C´ |
| 0 1 1 | 1 | A´ B C |
| 1 0 0 | 0 | |
| 1 0 1 | 0 | |
| 1 1 0 | 1 | A B C´ |
| 1 1 1 | 0 |
Tabelle 2 - Wahrheitstafel einer unbekannten
Schaltung mit den drei Eingangsvariablen
A, B und C und der Ausgangsgröße Q.
Die Minterme werden zu einer Gleichung zusammengefasst:
- Q = A´ B´ C + A´ B C´ + A´ B C + A B C´
und an der entsprechenden Stelle im KV-Diagramm durch Eintragung einer 1 vermerkt. Anschließend werden benachbarte Paare markiert, nach der Nachbarschaftsregel KV3.
Die einzelnen Minterme fasst man über das KV-Diagramm zusammen und erhält die Minimierung:
- Q = A´C + B C´.
Die zu dieser Gleichung gehörige digitale Schaltung besteht aus zwei AND- und einem OR-Gatter mit je einem invertierenden Eingang bei A und C.
3.1 - Übung: Aufbau einer Licht-Steuerung
| Übung: Aufbau einer Licht-Steuerung | |
| Aufgabe |
|
| Material |
|
Lösung
Gestartet wird mit der Aufstellung einer Wahrheitstabelle für die genannte Aufgabe. Dazu werden die drei Kreise mit A (Kreis 1), B (Kreis 2) und C (Kreis 3) benannt. Die Wahrheitstabelle sieht wie folgt aus:
|
Eingänge |
Gesamtleistung in W |
Minterm |
||
|
A |
B |
C |
|
|
|
0 |
0 |
0 |
0 |
|
|
0 |
0 |
1 |
2500 |
|
|
0 |
1 |
0 |
5000 |
|
|
0 |
1 |
1 |
7500 |
|
|
1 |
0 |
0 |
10.000 |
|
|
1 |
0 |
1 |
12.500 > 11.000 |
A B´ C |
|
1 |
1 |
0 |
15.000 > 11.000 |
A B C´ |
|
1 |
1 |
1 |
17.500 > 11.000 |
A B C |
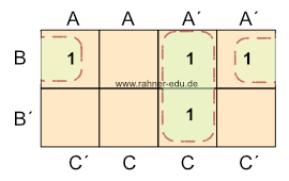
Übertragung der Ergebnisse aus der Wahrheitstabelle in ein KV-Diagramm:
Aus der KV3-Tabelle ergibt sich die minimierte Gleichung
- Q = AB + AC
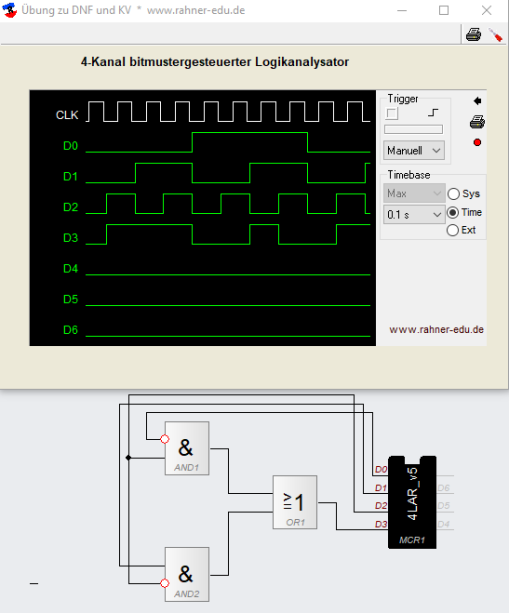
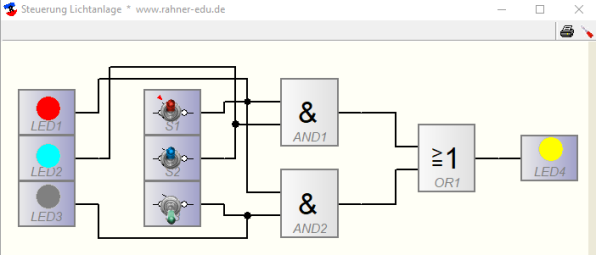
aus der sich die Steuerungsschaltung ableitet; sie enthält zwei AND- und ein OR-Gatter.
Schaltungsaufbau