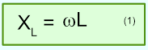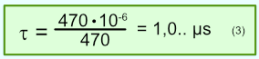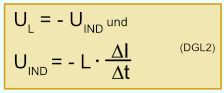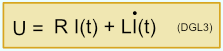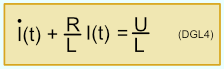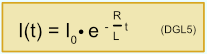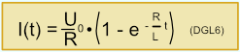1 - RL-Schaltung
RL-Schaltungen beeinflussen - wie auch RC-Schaltungen - das Frequenzverhalten von Signalen. Die Spule in einer RL-Schaltung besteht im Wesentlichen nur aus einem aufgewickelten Draht. Ist er stromdurchflossen, bildet sich ein Magnetfeld aus, dessen magnetische Wirkung erhebliche Auswirkungen hat. Dies wird in den folgenden Übungen näher angeschaut und untersucht.
Sein Wert hängt von der Frequenz f und dem Induktivitätswert L ab. Der formelmäßige Zusammenhang lautet:
Der Formel ist zu entnehmen:
- je höher die angelegte Frequenz, desto größer wird der Blindwiderstand XL.
- je größer die Induktivität L der Spule, desto größer wird der Blindwiderstand XL.
- ist die Frequenz f der anliegenden Wechselspannung identisch 0 (Gleichspannung), dann wird der Blindwiderstand identisch 0 und die Induktivität verhält sich rein ohmsch.
Übung 1 - Spule im Gleichstromkreis (1)
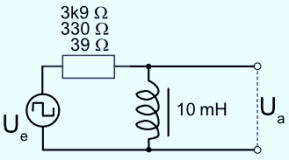
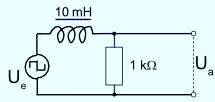
Eine periodisch auftretende Gleichspannung (Rechteckspannung) Ue wird an einen RL-Kreis gelegt und das Verhalten der Spannung Ua über der Induktivität untersucht.
| Spule im Gleichstromkreis | |
| Material |
|
| Aufgaben |
|
Schaltskizze
Abb. 1 - Das Rechtecksignal wird von einem Mikrocontroller per Programm erzeugt und an den RL-Kreis gelegt.
Das Programm lr_kreis_gleichspannung.c
Abb. 2 - Programm zur Ansteuerung eines RL-Kreises.
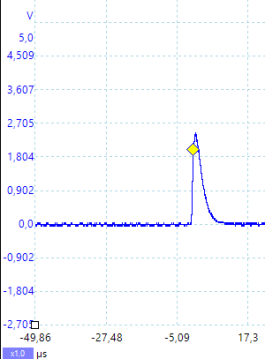
Die Ergebnisse
Abb. 2
Das Magnetfeld der Spule wird sehr schnell aufgebaut. Dem Graphen ist eine Zeit von ca. 7 µs zu entnehmen. ( R = 3k9 Ohm, L = 10 mH )
Abb. 4 - Bei R = 330 Ohm, L = 10 mH wird das Magnetfeld langsam aufgebaut (ca. 80 µs).
Beschreibung und Deutung der Ergebnisse
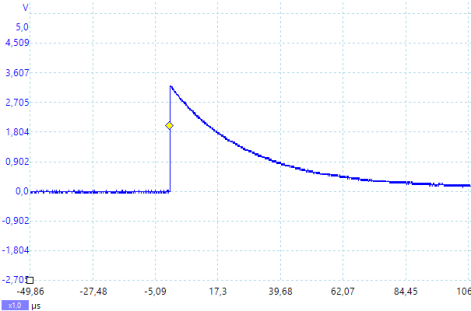
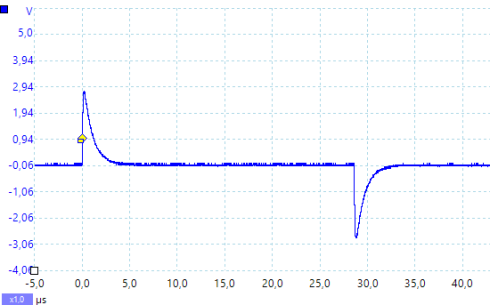
Die angelegte Rechteckspannung wirkt wie ein mechanischer Schalter. Solange der Schalter geschlossen ist (die Rechteckspannung auf HIGH gezogen ist), liegt an der Schaltung eine Gleichspannung von ca. 3,3 Volt an. Wird der Schalter geöffnet (die Rechteckspannung wird auf LOW gezogen), liegen 0 Volt an.
Solange die Schaltung auf HIGH oder auf LOW liegt, ist der gesamte Widerstand R in der Schaltung der Wirkwiderstand.
Interessant wird es an den beiden Stellen, wo der Schalter geöffnet (die Rechteckspannung von HIGH auf LOW geht) oder geschlossen wird (von LOW auf HIGH gezogen wird).
Zustandsänderung von LOW nach HIGH (Einschalten)
Die Spule ist anfangs stromlos. Nach der Zustandsänderung setzt ein Stromfluss ein, der eine magnetische Durchflutung und einen magnetischen Fluss im Magnetkreis der Spule bewirkt. Die Flussänderung von Null auf einen Wert bestimmten Wert führt zu einer Induktionsspannung (Selbstinduktion). Ursache dafür ist die Stromänderung. Die Induktionsspannung will den Stromanstieg verhindern und verzögert damit den Aufbau eines Magnetfeldes in der Spule (Stichwort: Lorenzkraft).
Der Aufbau des Magnetfeldes dauert um so länger, je kleiner der Widerstand R in der Schaltung ist.
Zustandsänderung von HIGH nach LOW (Ausschalten)
Liegt an der RL-Schaltung eine Gleichspannung von ca. 3,3 Volt an, dann wird sie von einem Gleichstrom durchflossen, das Magnetfeld in der Spule mit der Induktivität L ist aufgebaut. Das Abschalten der Spannung führt zu einer Stromänderung und dies wiederum zu einer Induktionsspannung Uind, die den Stromfluss weiter aufrecht erhalten möchte. Uind ist anfangs maximal und fällt dann stark ab. Sie wird Null, wenn die im Magnetfeld der Spule gespeicherte Energie im Widerstand R vollständig in Wärme umgesetzt wurde.
Eine Induktivität reagiert immer so, dass sie den Ist-Zustand erhalten möchte.
Abschließend zeigt Abb. 4a den Ein- und Ausschaltvorgang einer Spule bei Speisung über einen Controller-Port (Rechteckspannung).
Abb. 4a - Ein- und Ausschaltvorgang einer Spule, die von einer Rechteckspannung gespeist wird.
Übung 2 - Spule im Gleichstromkreis (2)
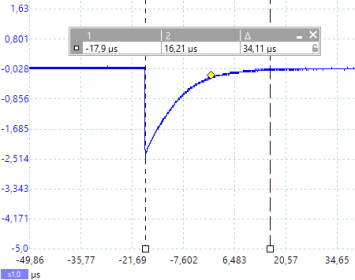
- In dieser Übung werden im Schaltkreis nach Abb. 1 Spulen mit verschiedenen Induktivitäten (L1 = 10 µH, L2 = 100 µH, L3 = 470 µH) eingesetzt, die jeweilige Spannung UL gemessen und die Abhängigkeit der Ladezeit von der Induktivität bestimmt. Der ohmsche Widerstand ist R = 39 Ohm.
Messergebnisse
Abb. 5 - R = 39 Ohm, L = 10 µH
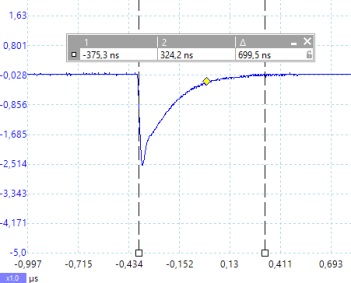
Die Ladezeit für das magnetische Feld der Spule liegt bei ca. 700 ns.
Abb. 6 - R = 39 Ohm, L = 100 µH
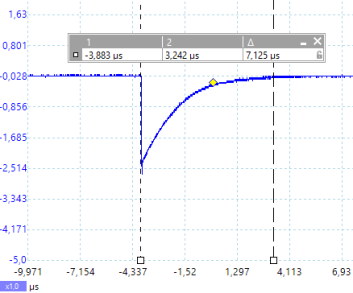
Die Ladezeit für das magnetische Feld der Spule liegt bei ca. 7 µs oder 7000 ns.
Abb. 7 - R = 39 Ohm, L = 470 µH
Die Ladezeit für das magnetische Feld der Spule liegt bei ca. 34 µs; das ist das 4,7-fache der Zeit, die eine Spule der Induktivität von 100 µH benötigt.
Die Zeit t für den Aufbau des Magnetfeldes in einer Spule ist direkt proportional zu seiner Induktivität.
Ergebnis
Aus beiden Übungen ergibt sich, dass die Zeit t für den Aufbau eines Magnetfeldes in einer Spule direkt proportional zur Induktivität L und umgekehrt proportional zum ohmschen Widerstand R in der Schaltung ist. Wir bezeichnen sie zukünftig als Zeitkonstante mit dem griechischen Buchstaben Tau.
R ist immer die Summe aus Gleichstromwiderstand der Spule und dem vorgeschalteten Widerstand.
Was man weiß, was man wissen sollte
Die Selbstinduktionsspannung Uind hängt von den Aufbaugrößen einer Spule und der Änderungsgeschwindigkeit des die Spule durchfließenden Stromes I ab. Es gilt:
Die im Magnetfeld einer Spule gespeicherte Energie W errechnet sich über die Gleichung
dabei bedeuten: W - Energie der Spule, L - Induktivität, I - Stromstärke
Übung 3 - Bestimmung der Zeitkonstanten
| Bestimmung der Zeitkonstanten | |
| Material |
|
| Aufgaben |
|
Lösungen
Rechnerisch ergibt sich nach Formel (2) für die Zeitkonstante mit den vorgegebenen Werten
Experimentelle Überprüfung der Zeitkonstanten
Die Zeitkonstante gibt an, nach welcher Zeit das Magnetfeld in der Spule auf 63% seines Maximalwertes angewachsen ist.
Zur Vorgehensweise im Versuch:
- Das Programm wird so verändert, dass bei Programmstart für 3s die Schaltung auf LOW liegt und anschließend für 3s auf HIGH gezogen wird.
- Das Oszilloskop wird mit der Impulsänderung von LOW nach HIGH getriggert. Aus dem Oszillogramm kann die Zeit abgelesen werden, bis zu der Uind auf 63 % seines Maximalwertes abgesunken ist; es ist die gesuchte Zeitkonstante.
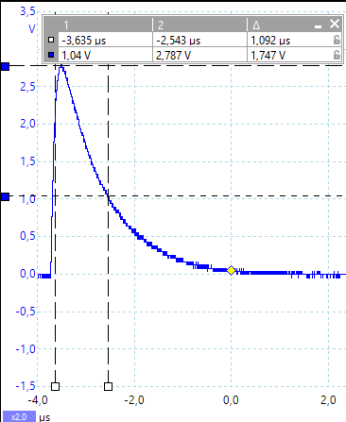
Messergebnis
Abb. 8 - Bestimmung der Zeitkonstante in einer RL-Schaltung mit R = 470 Ohm und L = 470 uH.
Fehlerabschätzung
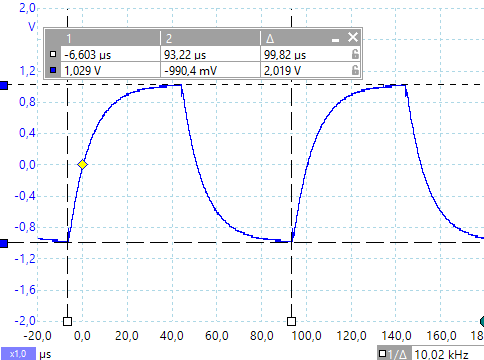
Dem Oszillogramm ist zu entnehmen, dass Uind bei ca. 2,78 V liegt. Wenn die Spannung um 63% abgefallen ist, entspricht das einer Größe von ca. 1,04 Volt. Der Spannungsabfall zwischen diesen beiden Marken kann aus dem Oszillogramm abgelesen werden und liegt bei ca. 1,09 µs.
- Die experimentell ermittelte Zeitkonstante von 1,09 µs entspricht der rechnerisch ermittelten Größe von 1,0.. µs.
Berücksichtigt man, dass die Spule nach Herstellerangabe eine Fehlertoleranz von +/- 10%, der ohmsche Widerstand von 5% hat und der ohmsche Spulenwiderstand mit 0,7 Ohm angegeben ist, dann liegt der Messwert im Fehlertoleranzbereich.
Übung 4 - Stromverlauf in einer Spule
| Stromverlauf in einer Spule | |
| Material |
|
| Aufgaben |
|
Schaltskizze
Messergebnis
Abb. 9 - Zeitlicher Verlauf der Stromstärke beim Ein- und Ausschalten eines Stromkreises mit Spule L = 10 mH und Widerstand R = 1000 Ohm bei f = 10,02 kHz.
Aufstellung der Differentialgleichung
Die im Oszillogramm dargestellte I-t-Funktion erhält man durch Aufstellung einer Differentialgleichung (DGL), bei der R der ohmsche Widerstand und L die Induktivität der Spule in der Schaltung ist. Dabei gilt:
und
Einsetzen von UL und UIND in (DGL1) ergibt
Umstellen der Gleichung ergibt die gesuchte DGL
Unter Berücksichtigung der Bedingungen für den Einschaltvorgang mit I(0) = 0 bzw. den Ausschaltvorgang mit I(0) = I0 ergibt sich als Lösung der DGL:
für den Ausschaltvorgang, wobei I0 der maximale Strom zur Zeit t = 0 ist und
für den Einschaltvorgang, wobei der Quotient Uo/R der Stromstärke entspricht, die sich nach einer Zeit t, mit t beliebig groß, einstellt. R ist der Widerstand im Kreis und L die Induktivität der Spule..
Experimentelle Bestimmung der Zeitkonstante (2. Methode)
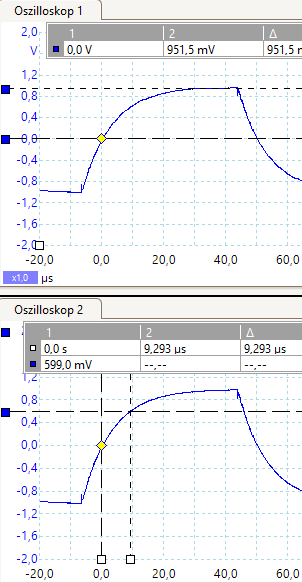
Dem Oszillogramm (siehe Abb. 10, 11) lassen sich alle notwendigen Daten zur Bestimmung entnehmen.
Abbildung 10
Experimentelle Bestimmung der Zeitkonstante in einem LR-Kreis.
Aus der oberen Abbildung (Oszilloskop 1) kann die maximale Spannung von 951,5 mV abgelesen werden. 63% von 951,5 mV entsprechen 599 mV.
Abbildung 11
Dort wo das Zeitlineal in der unteren Abbildung (Oszilloskop 2) das horizontale Spannungslineal kreuzt, hat die Stromstärke im Schaltkreis 63% vom Maximalwert erreicht. Dies ist nach ca. 9,3 µs der Fall. Experimentell liegt die Zeitkonstante bei ca. 9,3 µs.
Unter Berücksichtigung der Bauteiletoleranzen (10% bei der Induktivität und 5% beim ohmschen Widerstand) ist das ein guter Wert.
Der rechnerische Wert der Zeitkonstante ergibt sich nach (2) zu 10 µs.
Druckversion 