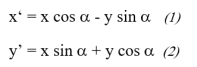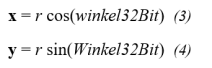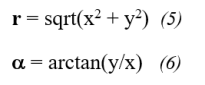SPIN2 und Propeller P2
Mathematische Methoden
Die in SPIN2 bereitgestellten sieben mathematischen Methoden:
- rotxy(x,y,winkel32Bit): x,y
- polxy(length, winkel32Bit): x,y
- xypol(x,y): length, winkel32Bit
- qsin(length, winkel, twoPi): y
- qcos(length, winkel, twoPi): x
- muldiv64(fakt1, fakt2, divisor): quotient
- getrnd(): rnd
sind ausschließlich für Ganzzahlarithmetik ausgelegt. Das heißt, Fließkommazahlen oder reelle Zahlen lassen sich damit nicht direkt verarbeiten.
Blau unterlegt sind die Eingabeparameter, grün die Ausgabegrößen.
Einzelne Methoden werden wir uns in den folgenden Übungen etwas näher anschauen.
Übung 1 – Die Methoden rotxy und polxy
Starten wir mit einem kurzen Theorieteil
a - Die Methode ROTXY
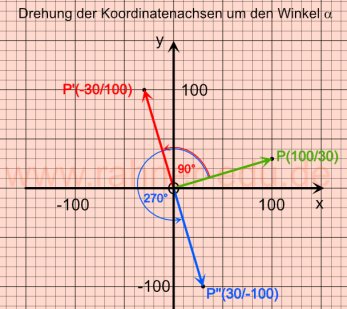
Bei der Methode rotxy werden die Koordinaten eines Ortsvektors rP mit den Koordinaten (x/y), der um alpha-Grad entgegen dem Uhrzeigersinn gedreht wird, berechnet und im Debug Output Fenster dargestellt.
Die Transformationsgleichungen für die Drehung eines Ortsvektors rP um den Winkel alpha lauten:
An den Transformationsgleichungen (1) und (2) erkennt man sofort, dass bei einer Drehung um 90° die x- und y-Koordinaten ihre Position vertauschen und das Vorzeichen der neuen x-Koordinate invertiert wird. So wird zum Beispiel aus
- P(100/30) nach einer 90° Drehung: P‘(- 30/100)
- P(100/30) nach 270° Drehung (entspricht: 3x 90° Drehung): P(100/30) - Drehung um 90° - P‘(-30/100) – Drehung um noch einmal 90° P‘‘(-100/-30) - nochmals Drehung um 90° - P‘‘‘(30/-100).
b - Die Methode POLXY
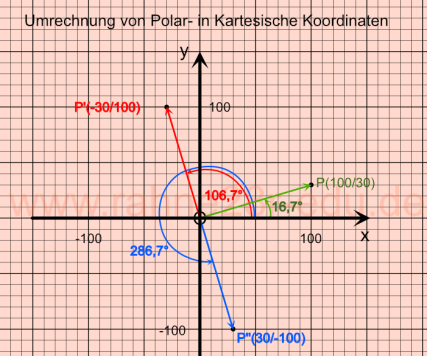
Die Methode polxy rechnet die Polarkoordinaten eines Punktes P(r, winkel32Bit) in kartesische Koordinaten P(x,y) um. Die Transformationsgleichungen dafür lauten:
Über die Transformationsgleichung (3) und (4) lassen sich die kartesischen Koordinaten mit Hilfe eines Taschenrechners ermitteln. Diese Werte werden anschließend mit den Werten verglichen, die über POLXY in SPIN2 im Debug Output Fenster angezeigt werden.
Der Parameter winkel32Bit von POLXY besagt, dass einem vollen Winkel (360° oder 2Pi) die höchste 32-Bitzahl entspricht:
- 360° entsprechen 232 = 4.294.967.296 = $FFFFFFFF
- 1° entspricht damit dem 360.Teil von $FFFFFFFF oder $B60B61
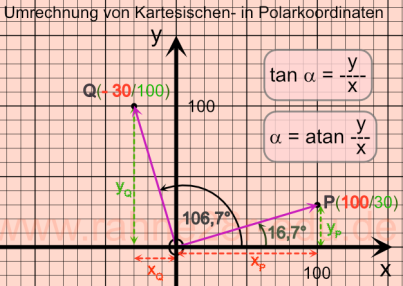
Abb. 1a korrespondiert mit Abb. 1b. Eine Drehung des Ortsvektors rP(104,4/16,7°) um 90° entspricht einem Ortsvektor rP' (104,4/106,7°). Die kartesischen Koordinaten lassen sich in diesem Fall direkt aus Abb. 1b ablesen: rP(100/30) und rP'(-30/100). Für die Polarkoordinaten der anderen Ortsvektoren gilt das gleiche Verfahren.
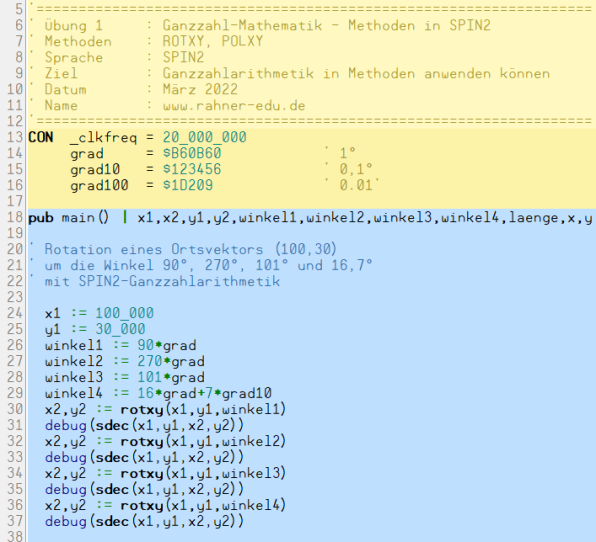
Das Programm rotxy_polxy.spin2
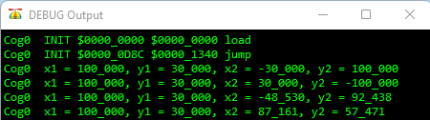
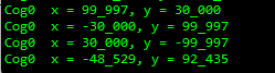
Debug Output Anzeige ROTXY - Erhöhung der Rechengenauigkeit
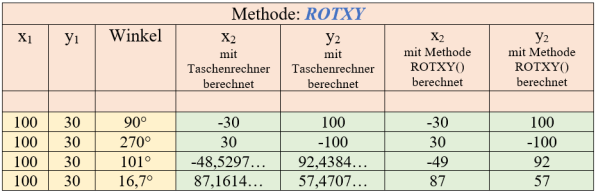
Würdigung der Ergebnisse mit der Methode ROTXY
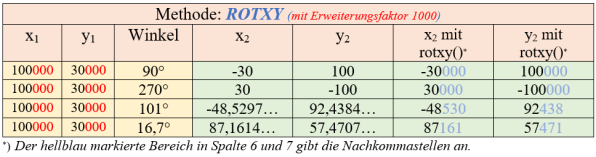
Die nachfolgende Abb. 4a stellt für verschiedene Winkel die mit einem Taschenrechner errechneten Werte den über die Methoden ROTXY in SPIN2 berechneten Werten gegenüber.
Durch die Ganzzahlarithmetik werden die auf Einer gerundeten Werte von x2 und y2 angezeigt. Die Genauigkeit lässt sich dadurch erhöhen, dass man die Eingabewerte x1, y1 mit einer frei gewählten Zehnerpotenz erweitert.
Sollen die mit ROTXY errechneten Werte zum Beispiel drei Nachkommastellen ausgeben, wobei die dritte Stelle dann wieder gerundet sein wird, müssen die Eingabewerte um den Faktor 1000 erhöht werden. Die Ergebnisse zeigt Abb. 4b.
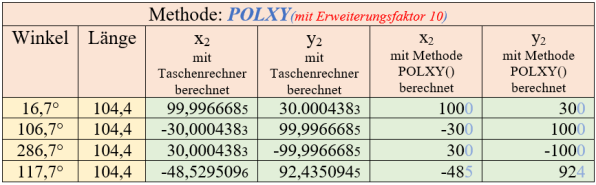
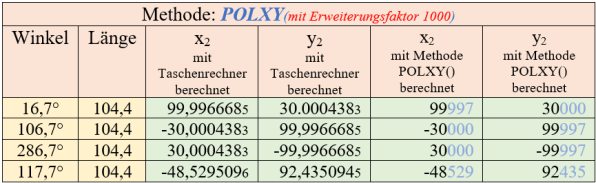
Debug Output Anzeige POLXY - Erhöhte Rechengenauigkeit
Würdigung der Ergebnisse mit der Methode POLXY
Die nachfolgende Abb. 4a stellt für verschiedene Winkel, die mit einem Taschenrechner errechneten Werte den über die Methode POLXY in SPIN2 berechneten Werten gegenüber.
Übung 2 – Die Methode xypol
Die Methode xypol rechnet die kartesischen Koordinaten eines Vektors in Polarkoordinaten um. Die Transformationsgleichungen lauten:
Mit dem nachfolgenden Programm werden die Polarkoordinaten eines Vektors r(x,y) berechnet und im Debug-Output Fenster angezeigt.
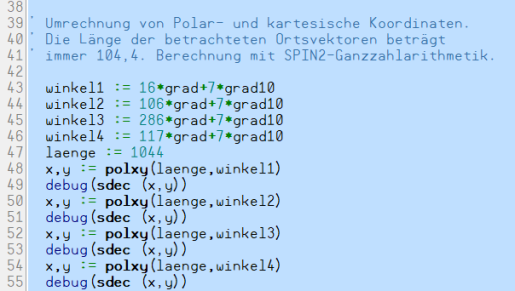
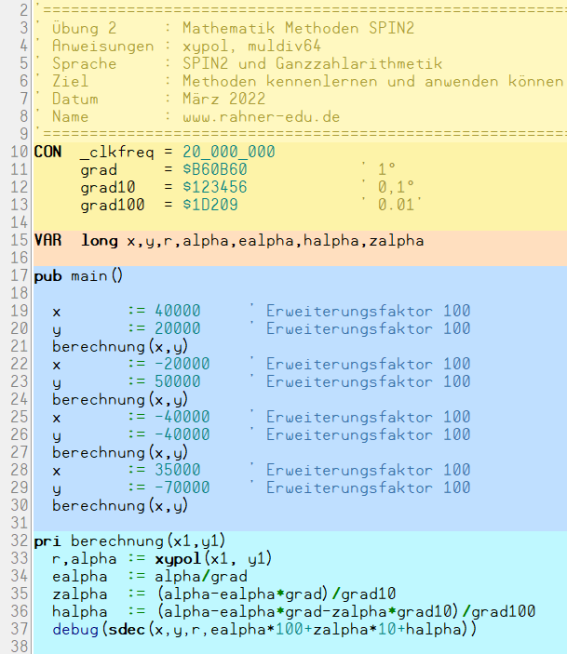
Das Programm xypol.spin2
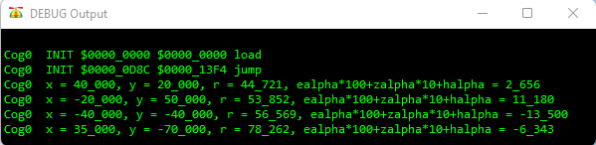
Debug Output Anzeige XYPOL - (erhöhte Rechengenauigkeit)
Würdigung der Ergebnisse mit der Methode XYPOL
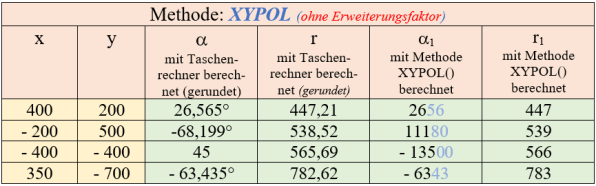
Die nachfolgende Abb. 8b stellt für verschiedene Winkel die mit einem Taschenrechner errechneten Werte den über die Methoden XYPOL in SPIN2 berechneten Werten gegenüber.
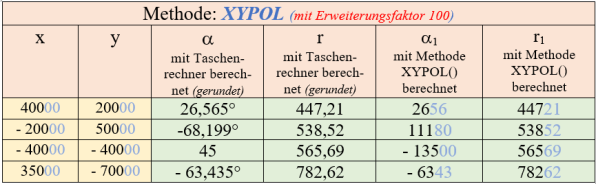
Abb. 8b - Die mit der Methode XYPOL berechneten Transformationswerte für verschiedene kartesische Koordinatenangaben. Bei der Winkelangabe in Spalte 5 geben die letzten beiden Ziffern (hellblau) die Nachkommastellen an. Die auf Einer gerundeten Längenwerte in Spalte 6 stimmen mit den Taschenrechner-Werten (gerundet) überein; gleiches gilt für die Winkelwerte.
Der Winkelwert wird über die arctan-Funktion berechnet, mit einer Periode Pi. Der Ortsvektor rP(-200/500) liegt im 2. Quadranten. Dem Taschenrechnerwert des Winkels von
| 68,199° | entspricht real der Ergänzungswinkel zu 180°; das sind 111,2°.
Der Ortsvektor rP(-400/-400) liegt im 3. Quadranten. Dem Taschenrechnerwert von
|45° | entspricht real der Winkel 225°. Dem mit XYPOL errechneten Winkelwert von |135°| entspricht der Ergänzungswinkel zu 360°; das sind ebenfalls 225°.
Der Ortsvektor rP(350/-700) liegt im 4. Quadranten. Dem Taschenrechnerwert von
|63,455° | entspricht real der Ergänzungswinkel zu 360°; das sind 296,57°.
Übung 3 – Die Methoden qsin und qcos
Die Methoden
- qsin(Skalierung, winkel°, wdezimalen360): y
- qcos(Skalierung, winkel°, wdezimalen360): x
berechnen den sin- bzw. cos-Wert zu einem gegebenen Winkel winkel°.
Bei ganzzahligen Winkeleingaben ist der Parameter wdezimalen360 gleich 360.
Die Nachkommastellen von y bzw. x lassen sich über Skalierung einstellen.
Bei Winkeleingaben mit Dezimalstellen, muss wdezimalen360 um die Anzahl der Nachkommastellen erweitert werden. Bei zwei Dezimalstellen auf 36000.
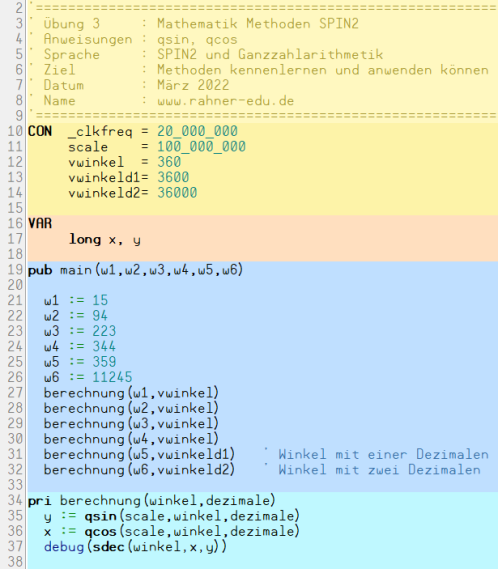
Schauen wir uns das in einem kleinen Programm sinCos.spin2 an und vergleichen anschließend die ermittelten Werte mit Taschenrechnerwerten.
Das Programm sinCos.spin20
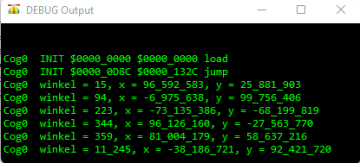
Debug Output Anzeige QSIN, QCOS
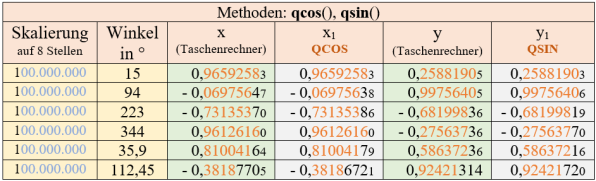
Würdigung der Ergebnisse mit den Methoden QSIN und QCOS
Die nachfolgende Abb. 9b stellt für verschiedene Winkel die mit einem Taschenrechner errechneten Werte den über die Methoden QSIN und QCOS in SPIN2 berechneten Werten gegenüber.
- Ganzzahlige Winkelwerte und Winkelangaben mit einer Dezimalen stimmen in sechs/sieben Dezimalen überein.
- Die Ergebnisse mit QSIN und QCOS werden ungenauer, sobald Winkel mit zwei Dezimalen benutzt werden. Die Abweichungen zum Taschenrechnerwert liegen dann bei <=| 0,01° |.