1 - Tiefpass
Diese Übung ist nur mit der BASIC Stamp und der Sprache PBASIC durchführbar, da sich die Inhalte auf spezifische Programmbefehle beziehen.
Im Gegensatz zu digitalen Signalen, die normalerweise zwischen 1(HIGH) und 0(LOW) pendeln, nehmen analoge Signale nicht nur HIGH oder LOW Zustände an, sondern auch alle dazwischen. Akustische Wellen, wie sie über Lautsprecher zum Beispiel abgegeben werden, setzen sich aus einer Vielzahl von Sinuswellen zusammen.
Mit einem Mikrocontroller lassen sich - obwohl er nur Nullen und Einsen an seine Ausgänge legt - auch Sinuswellen erzeugen. Ein Controller approximiert eine Sinuswelle durch eine Reihe von Rechteckschwingungen. Das werden wir uns jetzt genauer anschauen.
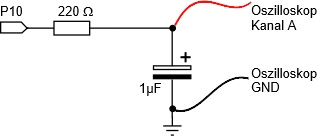
Servos werden durch feste Impulsfolgen gesteuert, die, je nach Drehrichtung und Geschwindigkeit des Servos, unterschiedliche und feste HIGH und LOW-Zeiten haben. In 2 - Zeitvariierende Pulsfolge messen haben wir uns gerade mit einer Impulsfolge beschäftigt, deren HIGH- und LOW-Signale zeitabhängig waren. Schickt man ein solches Signal durch einen RC-Filter (ein sogenannter Tiefpass), dann sieht man im Oszillogramm eine Gleichspannung die sich zwischen 0V und 5V bewegt. Erhöht sich das Tastverhältnis (Verhältnis Pulsdauer zu Pulsperiode), wächst auch der zeitliche Mittelwert der Gleichspannung.
Der BASIC Stamp Befehl freqout erzeugt eine Pulsfolge, die, in Verbindung mit einem Tiefpass, eine Sinuswelle approximiert. Die Sinuswelle kann bei entsprechend hoher Frequenz mit Hilfe eines Piezo-Lautsprechers ausgegeben werden. Der Befehl freqout enthält drei bzw. vier Parameter
-
FREQOUT pin, dauer, freq1 (optional , freq2 )
pin ist der benutzte I/O Pin (0-15) der BASIC Stamp
dauer (1 - 65535) bestimmt die Tonlänge in der Einheit ms; Zeiteinheit: 1ms
freq1 Frequenz in Hertz; der Frequenzbereich reicht von 0 - 32767 Hz
freq2 optinale zweite Frequenz in Hertz
| Material |
1x Board of Education BS2 1x Widerstand, 220 Ohm (rot-rot-braun) 1x Elektrolyt. Kondensator, 1,0µF 6x Steckdraht |
| Aufgaben |
|
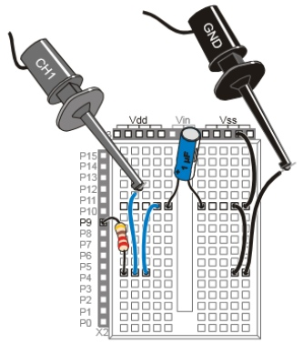
Schaltskizze und Schaltungsaufbau
Abbildung 1 - Tiefpassfilter
Abbildung 2 - Schaltungsaufbau Tiefpass auf Steckbrett
Das Programm Sinus1.bs2
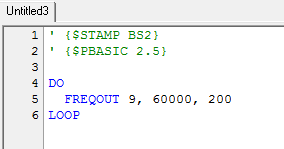
Programm Sinus1.bs2
Abbildung 3 - FREQOUT 9, 60000, 200 - Messwerte: f = 200,3Hz, Vss = 4,882V
|
Aufgaben- block 2 |
|
Lösungen zu Aufgabenblock 2
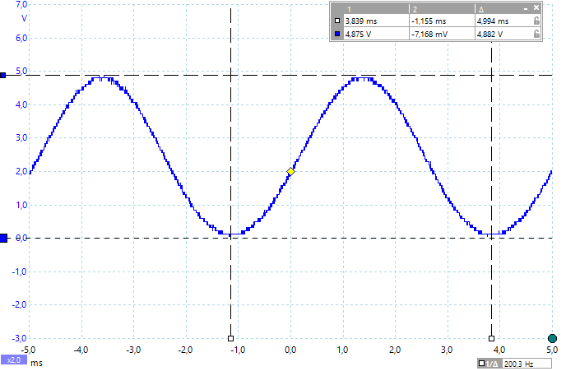
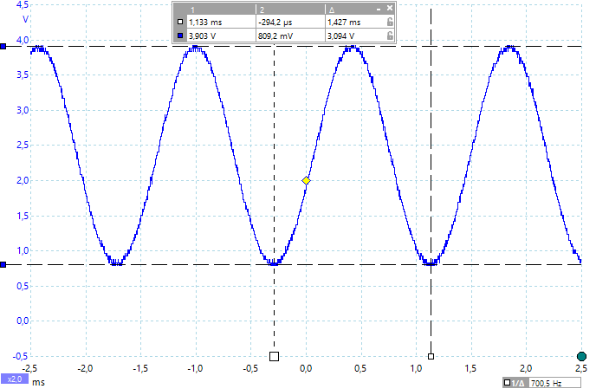
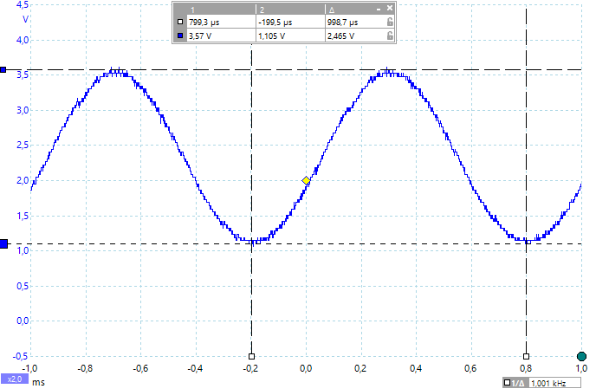
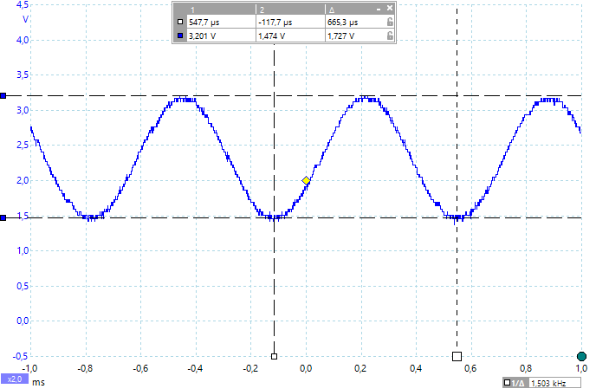
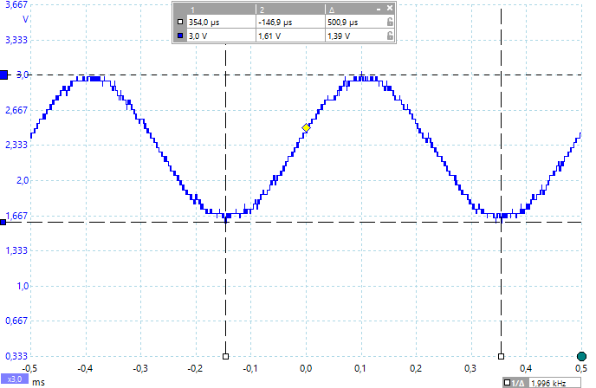
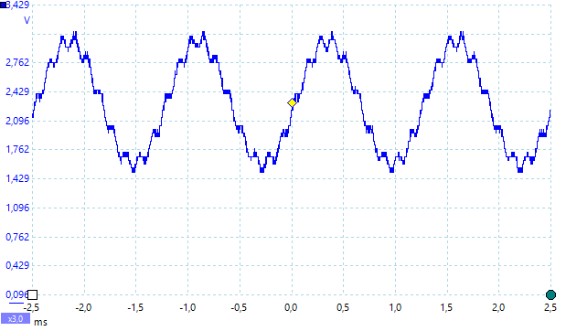
Dargestellt sind die entsprechenden Oszillogramme für die Frequenzen 700Hz, 1000Hz, 1500Hz, 2000Hz und 4000Hz. Die gemessenen Spannungswerte (Spitze-Spitze) und Frequenzen können im Bild abgelesen werden. Zu jedem Oszillogramm wird der entsprechende PBASIC Befehle freqout mit seinen Parametern benannt.
Abbildung 4 - FREQOUT 9, 60000, 700 - Messwerte: f = 700,5Hz, Vss = 3,094V
Abbildung 5 - FREQOUT 9, 60000, 1000 - Messwerte: f = 1000,1Hz, Vss = 2,465V
Abbildung 6 - FREQOUT 9, 60000, 1500 - Messwerte: f = 1500,3Hz, Vss = 1,727V
Abbildung 7 - FREQOUT 9, 60000, 2000 - Messwerte: f = 1996Hz, Vss = 1,39V
Abbildung 8 - FREQOUT 9, 60000, 4000 - Messwerte: f = 3996Hz, Vss = 780mV
Man sieht sehr deutlich, dass mit immer höherer Frequenz die Amplitude der Sinusschwingung stark abnimmt und die Frequenz dabei erhalten bleibt.
Ergebnis: Ein Tiefpassfilter lässt die tiefen Frequenzen ungehindert durch und filtert die hohen Frequenzen heraus.
2 - Messung zweier sich überlagernder Sinusschwingungen
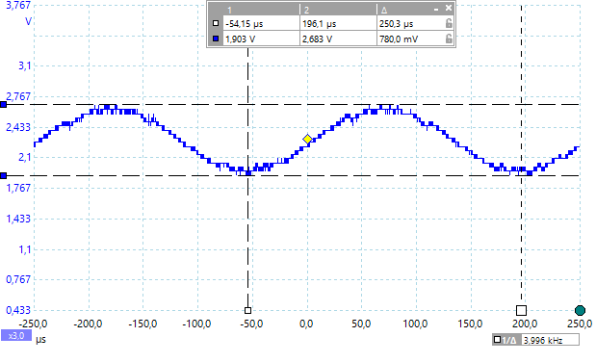
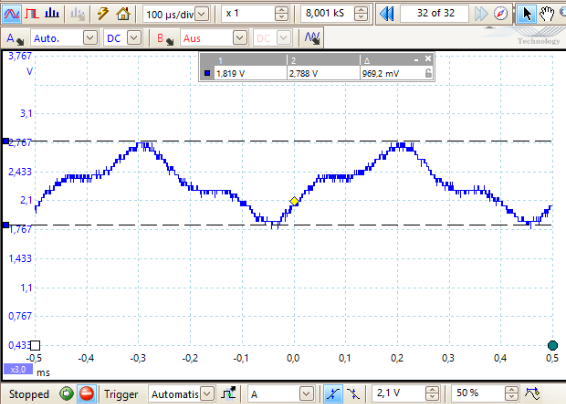
Mit dem Befehl FREQOUT haben wir die Möglichkeit zwei Sinusschwingungen unterschiedlicher Frequenz an einem I/O Pin zu erzeugen. Damit lassen sich dann Schwebungen oder auch nur zwei sich überlagernde Töne unterschiedlicher Frequenz, sogenannte Mischtöne, am Oszilloskop untersuchen. Und das werden wir jetzt tun.
| Material |
wie in 1 - Sinusschwingung Aufbau ebenfalls identisch |
|
Aufgaben- block 3 |
|
Das Programm Sinus_2.bs2
Darstellung auf dem Oszilloskop, im Programm PicoScope 6.0
Abbildung 9 - Oszillogramm zweier sich überlagernder Sinusschwinungen von 2kHz und 6kHz
3 - Fourier Transformation
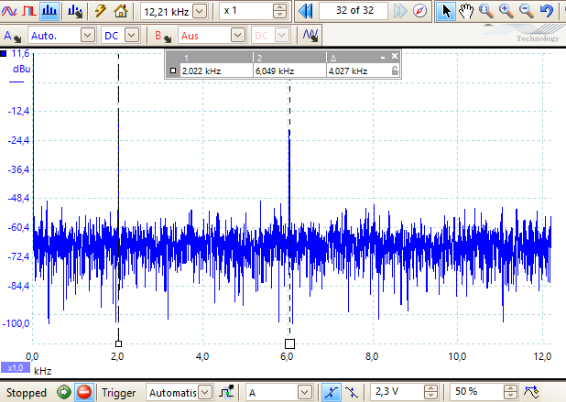
Das PicoScope-Programm emuliert einen Spektrumanalysator, in dem es die Frequenzen aller Sinusschwingungen darstellt, aus denen sich das im Oszillogramm dargestellte Signal zusammensetzt. Dies geschieht mit Hilfe der sogenannten Fourier Analysis, der Algorithmus nennt sich Fourier-Transformation. Mit ihrer Hilfe lassen sich zum Beispiel auch Resonanzen bei Motoren, Turbinen u.a. feststellen, die auf Dauer sonst ein Bauteil zerstören könnten.
Wir werden uns mit dem Spektrumanalysator das erzeugte Mischsignal anschauen und analysieren.
| Aufgaben |
|
Abbildung 10 - Fenster des Spektrumanalysators; es treten zwei Peaks bei 2kHz und 6kHz auf.
Jetzt kommst du!
| Aufgaben |
|
Abbildung 11 - Überlagerung zweier Sinusschwingungen der Frequenzen 800Hz und 8kHz
Druckversion 