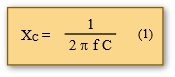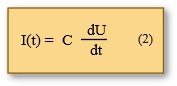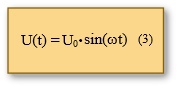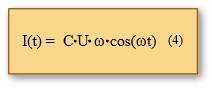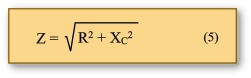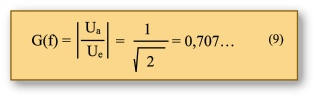1 - Passives RC-Glied
Im Kapitel Signale richtig verstehen - RC-Schaltung 2 wird mit einer RC-Schaltung gearbeitet und die Zeitkonstante bestimmt.
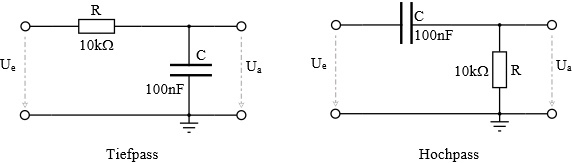
RC-Schaltungen beeinflussen das Frequenzverhalten von Signalen. Wie das aussieht, schauen wir uns am Beispiel von zwei passiven RC-Gliedern an - einem Tiefpass und einem Hochpass. Passiv im Gegensatz zu aktiv heißt, es gibt kein verstärkendes Element in der Schaltung und Tiefpass bzw. Hochpass deswegen, weil beim Tiefpass die tiefen und beim Hochpass die hohen Frequenzen durchgelassen und die hohen bzw. tiefen Frequenzen gesperrt werden.
Um dieses Verhalten zu verstehen, schaut man sich die Widerstände in der Schaltung an. Neben dem ohmschen Widerstand R gibt es noch einen kapazitiven Blindwiderstand XC.
Sein Wert hängt von der Frequenz und dem Kapazitätswert C ab. Der formelmäßige Zusammenhang lautet:
Der Formel ist zu entnehmen:
- je höher die angelegte Frequenz, desto kleiner wird der Stammbruch.
- je größer die Kapazität des Kondensators, desto kleiner wird der Stammbruch.
- Je kleiner der Stammbruch wird, desto kleiner wird der Blindwiderstand des Kondensators.
Eine weitere Eigenschaft des Kondensators ist, dass bei ihm die Stromstärke der Spannung vorauseilt. Dies ist leicht einzusehen, wenn man von einem völlig entladenen Kondensator ausgeht. Legt man ihn an eine Energiequelle, dann wird im ersten Moment ein hoher Ladungsstrom vorhanden sein, dessen Stärke mit der Zeit abnimmt. Je mehr Ladungen auf den Kondensatorplatten sind, desto mehr nimmt die Ladungsbewegung ab. Mit dem Ladungsfluss baut sich eine Spannung über den Platten auf.
Allgemein gilt für einen Kondensator der Kapazität C:
Legt man an den Kondensator eine sinusförmige Wechselspannung (3),
setzt diesen Term in (2) ein und leitet ihn nach der Zeit ab, dann bestätigt das Ergebnis die Phasenverschiebung zwischen Strom- und Spannungsgröße (die Funktionen sin(x) und cos(x) sind um 90° phasenverschoben).
Die Amplitude des Stromes hängt sowohl von der Frequenz f als auch von der Kapazität C ab.
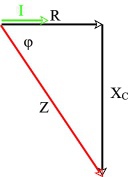
Der Scheinwiderstand Z zweier in Reihe geschalteter Widerstände R und Xc in einer Wechselstromschaltung ergibt sich aus dem Widerstandsdreieck. Er errechnet sich mit Hilfe des Satzes vom Pythagoras.
Danach gilt:
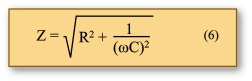
oder, wenn man für Xc nach Formel (1) einsetzt
2 - Amplituden-, Phasengang und Grenzfrequenz
für einen Tiefpass
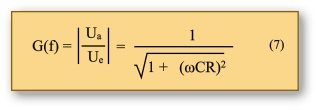
In den folgenden Versuchen wird die Abhängigkeit von Eingangs- und Ausgangsspannung (Ua/Ue) zur Frequenz (sogenannter Amplitudengang) bei einem Tiefpass untersucht. Den formelmäßigen Zusammenhang zeigt Gleichung (7)
Der Phasengang wird bestimmt durch
Ist der Spannungsabfall an R und Xc gleich groß, dann gilt für den Amplitudengang an dieser Stelle
Und wir schauen uns das Verhalten des Spannungsverlaufs am Ausgang an, wenn am Eingang eine Rechteckspannung angelegt wird.
3 - Erste Messungen am Tiefpass
| Erste Messungen am Tiefpass | |
| Material |
|
| Aufgaben |
|
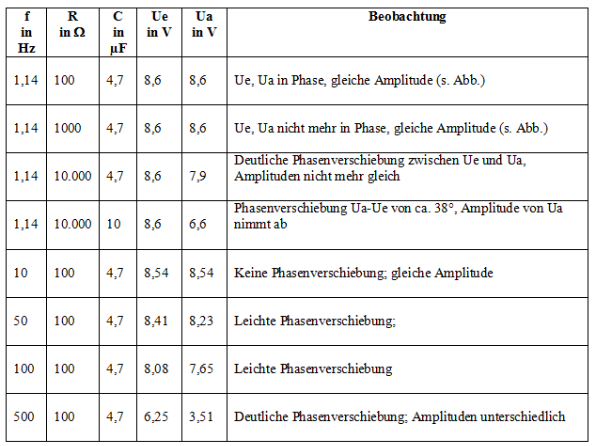
Mögliche Ergebnisse
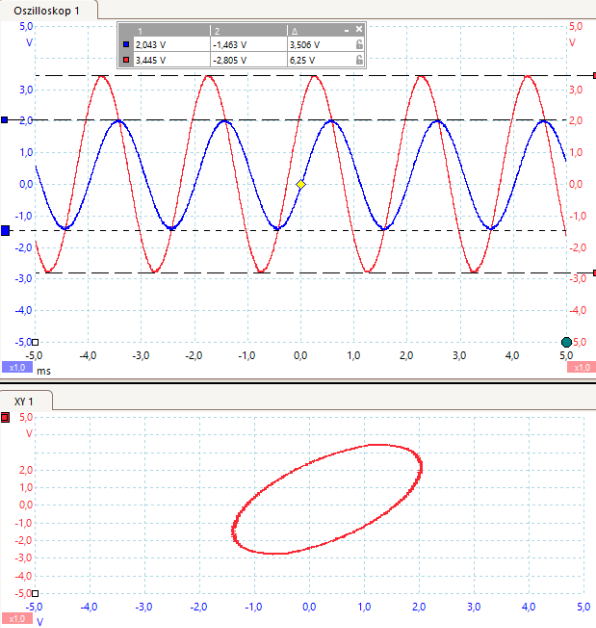
Bei niedriger Frequenz (ca. 1Hz) sind die Amplituden des Eingangs- und Ausgangssignals gleich groß und in Phase. Die Lissajous-Figur zeigt, dass die Phasenverschiebung zwischen Ua und Ue Null ist.
Bei einer Frequenz von 500Hz unterscheiden sich die Amplituden des Eingangs- und Ausgangssignals um den Faktor ca. 2; die Phasenverschiebung ist deutlich zu sehen. Auch dies wird von der Lissajous-Figur im unteren Bild bestätigt.
4 - Amplitudengang Tiefpass
| Durchlasskurve eines Tiefpasses ausmessen | |
| Material |
|
| Aufgabe |
|
| Ausführung |
|
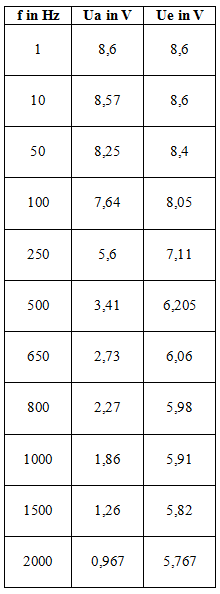
Mögliche Messergebnisse
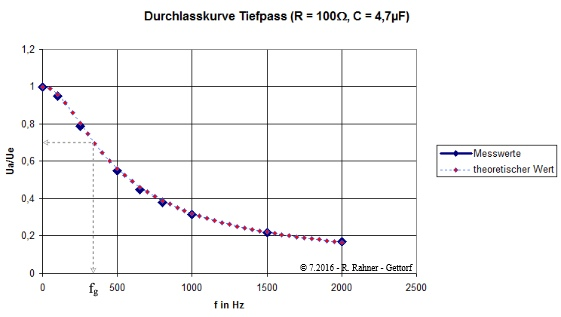
Für hohe Frequenzen wird der Widerstand des Kondensators immer kleiner, er wird durchlässig und damit geht die Ausgangsspannung immer stärker gegen Null. Im Graphen eingezeichnet ist die Grenzfrequenz, bei der die Widerstände R und Xc gleich groß sind und das Verhältnis von Aus- und Eingangsspannung einen Wert von 0,707 annimmt. Als rechnerischer Wert ergibt sich für die Grenzfrequenz fg ein Wert von 338Hz; dieser Wert ist experimentell gut bestätigt. Der Graph hat das folgende Aussehen:
5 - Amplituden-, Phasengang und Grenzfrequenz
für einen Hochpass
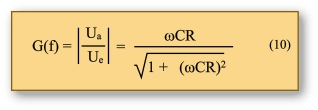
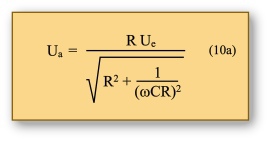
In den folgenden Versuchen wird die Abhängigkeit von Eingangs- und Ausgangsspannung (Ua/Ue) zur Frequenz (sogenannter Amplitudengang) bei einem Hochpass untersucht. Den formelmäßigen Zusammenhang zeigt Gleichung (10)
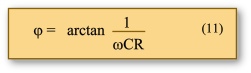
Der Phasengang wird bestimmt durch
6 - Hochpass
| Erste Messungen am Hochpass | |
| Material |
|
| Aufgaben |
|
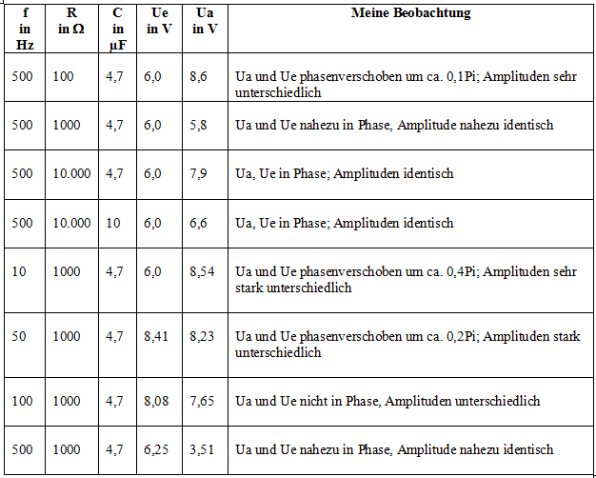
Mögliche Ergebnisse
7 - Amplitudengang Hochpass
| Amplitudengang Hochpass | |
| Material |
|
| Aufgabe |
|
| Ausführung |
|
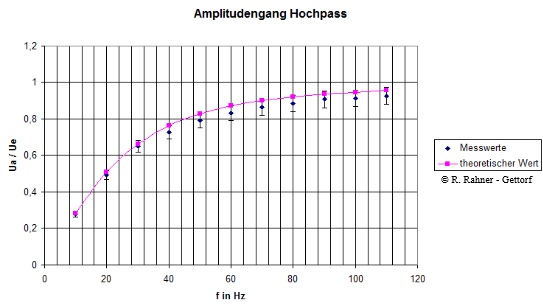
Mögliche Messwerte
Für hohe Frequenzen wird Xc klein gegenüber R; daraus folgt, dass Ua gegen Ue strebt oder anders ausgedrückt, die beiden Spannungswerte Ua und Ue gleichen einander an. Dies ist im Graphen deutlich zu sehen, lässt sich aber auch aus Gleichung (10) ableiten. Dazu wird die Gleichung etwas umgestellt, damit man den ohmschen Widerstand und den kapazitiven Blindwiderstand als Term besser erkennt.
Wird dagegen die Frequenz immer kleiner und Xc gegenüber R groß, strebt der Nenner in (10a) über alle Grenzen und damit strebt Ua gegen 0. Dies ist ebenfalls dem Graphen zu entnehmen.
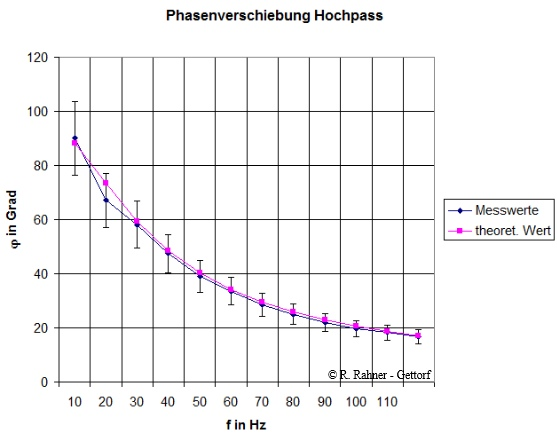
8 - Phasengang Hochpass
Bei den ersten Messungen aus RC Schaltung 1 - Übung 6 - Hochpass mit unterschiedlichen Kapazitätswerten des Kondensators und unterschiedlichen ohmschen Widerständen konnte die eintretende Phasenverschiebung zwischen der Aus- und Eingangsspannung beobachtet werden. Sie ergibt sich rechnerisch über die Formel (11).
Die Aufnahme des Phasengangs zeigt die folgende Abbildung.
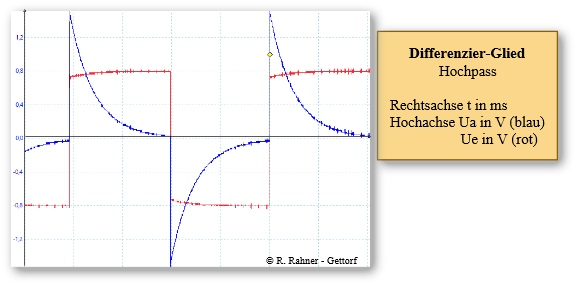
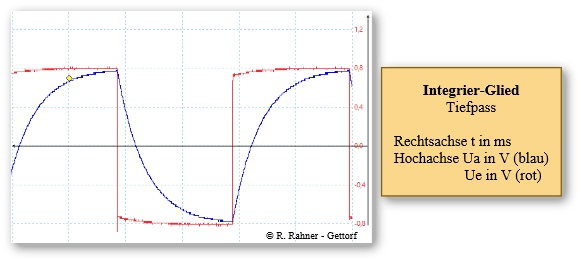
9 - Rechteckspannung am Hoch- und Tiefpass
Die beiden folgenden Oszillogramme zeigen die Spannungsverläufe bei einer angelegten Rechteckspannung. Die rote Kurve ist jeweils die Eingangsspannung, die blaue die Ausgangsspannung.