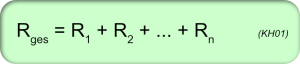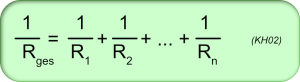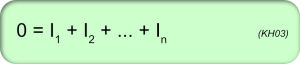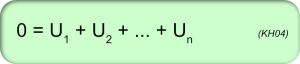Widerstandsnetzwerk 1
Parallel- und/oder Reihenschaltungen von Widerständen lassen sich auf Ersatzwiderstände reduzieren. Über das Ohmsche Gesetz werden die Formeln zur Berechnung des Gesamtwiderstandes einer Reihen- bzw. Parallelschaltung von Widerständen hergeleitet. Es gelten die folgenden Gesetze:
1 - Reihenschaltung von n Widerständen (n aus N)
Bei einer Reihenschaltung von Widerständen ist der Gesamtwiderstand gleich der Summe der einzelnen Widerstände.
2 - Parallelschaltung von n Widerständen (n aus N)
Der Ersatzwiderstand parallel geschalteter Widerstände ist immer kleiner als der kleinste in der Schaltung vorkommende Parallelwiderstand.
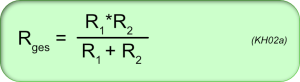
Auflösen von (KH02) nach Rges ergibt für zwei Widerstände die aus der Schule bekannte Formel
Nicht alle Reihen- oder Parallelschaltungen von Widerständen lassen sich auf Ersatzwiderstände reduzieren. Da kommen dann die Kirchhoff Gesetze ins Spiel.
3 - 1. Kirchhoff Gesetz (Knotenregel)
Für jeden Knoten eines Netzwerkes gilt, dass die Summe der Ströme, die zu einem Knoten hinfließt, gleich der Summe der Ströme ist, die von ihm wegfließt.
4 - 2. Kirchhoff Gesetz (Maschenregel)
Die Summe der Spannungen in einer Masche – bei beliebig festgelegtem Umlaufsinn – ist Null.
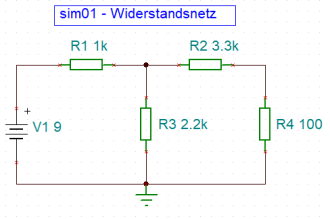
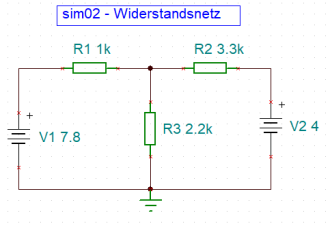
Soweit die eher trockene Theorie. Betrachten wir dazu eine DC-Beispielschaltung aus vier Widerständen und einer Energiequelle.
- Für die Berechnung der Teilgrößen einer Schaltung wird das Programm TINA in der derzeit aktuellen Version verwendet;
- die rein rechnerische Ermittlung der Teilgrößen erfolgt mit Hilfe des Werkzeugs Interpreter bzw. kann alternativ natürlich auch mit Hilfe eines Taschenrechners durchgeführt werden.
- die Simulationswerte werden über eine DC-Analyse ermittelt.
Übung 1 - DC Netzwerk - 1
a - Die Schaltskizze
Abb. 1
Schaltskizze zu Übung 1. Gegeben sind die Widerstandswerte:
R1 = 1 kOhm
R2 = 3,3 kOhm
R3 = 2,2 kOhm
R4 = 100 Ohm
und die Batteriespannung: Ubat = 9 V
Es sind alle Zweigströme und Teilspannungen zu berechnen.
b - Berechnung der Teilspannungen und Teilströme
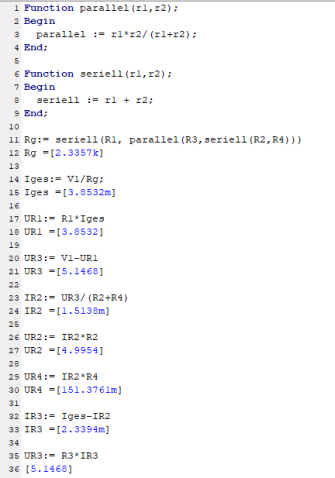
Die Berechnung der elektrischen Größen erfolgt mit Hilfe des Interpreters der Simulationssoftware TINA. Aufgerufen wird er über das Hauptmenü Werkzeuge - Interpreter.
Abb. 2
Der Interpreter wird über
- Werkzeuge -> Interpreter
aus dem Hauptmenü von TINA aufgerufen.
In Zeile 1 und Zeile 6 werden die beiden Funktionen
- parallel - für parallele Widerstände
und
- seriell - für Widerstände in Reihe
definiert.
Die Berechnungen gelten für den Idealfall Ri = 0.
Zeile 11ff: Bestimmung von Rg(esamt)
Zeile 14ff: Bestimmung von Iges = IR1
Zeile 17ff: Bestimmung von UR1
Zeile 20ff: Bestimmung von UR3
Zeile 23ff: Bestimmung von IR2
Zeile 26ff: Bestimmung von UR2
Zeile 29ff: Bestimmung von UR4
Zeile 32ff: Bestimmung von IR3
Zeile 35ff: Bestimmung von UR3
c - Simulation der Schaltung
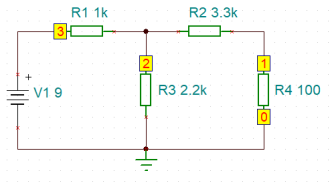
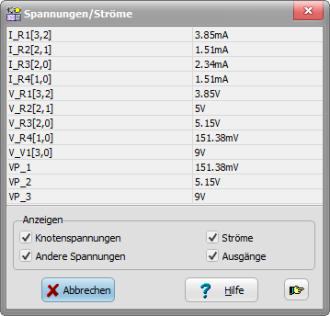
Über das Hauptmenü ANALYSE - Tabelle der DC Ergebnisse werden alle Teilergebnisse des Widerstandsnetzes aus Abb. 1 tabellarisch erfasst. In der Schaltskizze (s. Abb. 3) werden automatisch Knotenpunkte von 0 ... 3 eingetragen, auf die die Beschriftung in der DC-Tabelle (s. Abb. 4) Bezug nimmt.
Abb. 3
Die Knotenpunkte 0 ... 3 werden automatisch gesetzt beim Aufruf von Analyse - DC Analyse.
So bezeichnet V_R1[3,2] die Spannung über R1 und I_R2[2,1 ]die Stromstärke durch R2 von Punkt 2 nach Punkt 1 in der Schaltung. Die Potentiale an den Punkten x, mit x aus {1,2,3}, werden durch VP_x angezeigt.
Abb. 4
DC-Analysewerte zur Schaltung aus Abb. 1.
Die errechneten elektrischen Größen stimmen mit den vom Simulationsprogramm ermittelten Werten überein.
Übung 2 - DC Netzwerk - 2
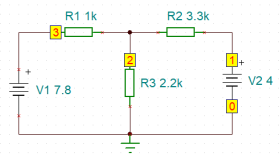
a - Die Schaltskizze
Abb. 5 - Schaltskizze zu Übung 2
In diesem Netzwerk befinden sich zwei Spannungsquellen.
Gegeben sind die Widerstandswerte:
R1 = 1 kOhm
R2 = 3,3 kOhm
R3 = 2,2 kOhm
und die Batterien:
V1 = 7,8 V
V2 = 4 V
Es sind alle Zweigströme und Teilspannungen zu berechnen.
b - Das Überlagerungsverfahren
Im vorliegenden Netzwerk befinden sich ausschließlich lineare Bauteile (ohmsche Widerstände) sowie zwei Spannungsquellen, keine Stromquelle. Darauf kann das Überlagerungsverfahren angewendet werden. Befinden sich auch nichtlineare Bauteile (z.B. Kondensatoren, Dioden, Transistoren etc.) in der Schaltung, kann diese Methode nicht verwendet werden.
Das Verfahren besteht aus vier Arbeitsschritten:
- Jede Spannungsquelle, jede Stromquelle wird einzeln betrachtet (dabei werden alle anderen Spannungsquellen kurzgeschlossen oder überbrückt; bei Stromquellen werden die Stellen in der Schaltskizze unterbrochen).
- Es ergibt sich für jede Quelle ein Ersatzschaltbild.
- alle Zweigströme und Teilspannungen in der Ersatzschaltung werden berechnet.
- Zum Schluss werden alle Teilgrößen addiert (überlagert).
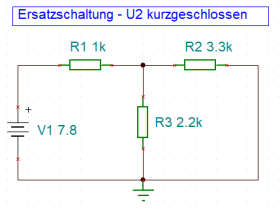
Für die Schaltung aus Abb. 5 mit zwei Spannungsquellen müssen über zwei Ersatzschaltbilder separat alle Teilströme bestimmt werden.
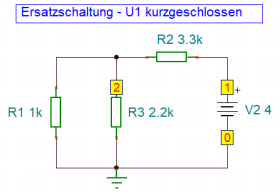
1a - Spannungsquelle V2 wird kurzgeschlossen
Abb. 6a
Ersatzschaltung für die kurzgeschlossene Spannungsquelle V2. In diesem Fall liegen R2 und R3 parallel zueinander und in Reihe mit R1 (s. Abb. 6b).
Abb. 6b
R2 und R3 liegen parallel zueinander und in Reihe zum Widerstand R1.
Die Teilgrößen Ersatzwiderstand Rg1A und Gesamtstromstärke Ig1A werden mit dem Interpreter des Simulationsprogramms berechnet.
Abb. 7
Ersatzwiderstand Rg1A und Gesamtstromstärke Ig1A:
- Rg1A = 2,32 kOhm.
- Ig1A = I1A = 3,36 mA
Mit Hilfe des Ohmschen Gesetzes lassen sich die Teilströme I2A und I3A berechnen:
Abb. 8
Berechnung der Teilstromstärken:
- I2A = -1,345 mA
- I3A = 2,02 mA
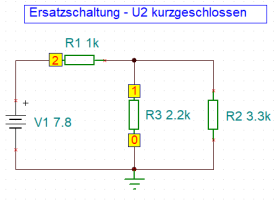
1b - Spannungsquelle V1 wird kurzgeschlossen
Abb. 9
R1 und R3 liegen parallel zueinander und in Reihe zum Widerstand R2.
Die Berechnungen der Teilstromstärken I1B, I2B und I3B wird analog wie bei der vorherigen Ersatzschaltung durchgeführt. Es ergeben sich rechnerisch die folgenden Werte:
Abb. 10
Berechnung der Teilstromstärken:
- I1B = -689,655 µA
- I2B = 1,003 mA
- I3B = 313,48 µA
Im letzten Schritt werden die entsprechenden Teilstromstärken der beiden Ersatzschaltungen addiert und ergeben die gesuchten Größen der Schaltung in Abb. 5.
- I1A = 3,36 mA, I1B = -0,69 mA
- I2A = -1,35 mA, I2B = 1,003 mA
- I3A = 2,02 mA, I3B = 0,313 mA
Die Teilstromstärken errechnen sich zu:
- I1 = I1A + I1B = 2,67 mA
- I2 = I2A + I2B = - 0,342 mA
- I3 = I3A + I3B = 2,33 mA
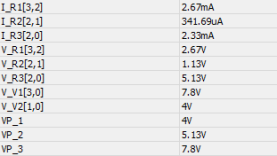
Vergleichen wir abschließend die errechneten Werte mit den Werten, die das Simulationsprogramm berechnet. Dazu wird im Simulationsprogramm über das Hauptmenü Analyse -> DC - Analyse -> Tabelle der DC Ergebnisse aufgerufen.
DC-Analyse mit einem Simulationsprogramm
Abb. 11a
DC-Analyse mit eingetragenen Knotenpunkten in der Schaltskizze.
Abb. 11b
DC Analysewerte der Schaltung aus Abb. 11a.
Würdigung der Simulationsergebnisse
Die ermittelten DC-Analysewerte sind - bis auf ein Vorzeichen - identisch. Die Abweichung im Vorzeichen kommt dadurch zustande, dass eine bestimmte Stromrichtung beim rechnerischen Ansatz vorgegeben wird. Bei der rechnerischen Ermittlung galt für die Teilströme
- I3 = I1 + I2. oder in der Notation nach Abb. 11a
- I_R3[2,0] = I_R1[3,2] + I_R2[1,2]
Das Simulationsprogramm berechnet nicht I_R2[1,2] sondern I_R2[2,1], kehrt also die Stromrichtung um. Daher die Abweichung; die Ergebnisse sind identisch.
Druckversion 