Digitaltechnik – 1
1 - Schaltalgebra
Im Kapitel Digitaltechnik - 0 wurden die Schaltzeichen und Wahrheitstabellen des AND-, NAND-, OR-, NOR-, XOR- und NON-Gatters vorgestellt. In diesem Abschnitt geht es um die Erfassung der Gesetze der Schaltalgebra mit Hilfe eines Bitmustergenerators und Logikanalysators auf Software-Basis (ProfiLab Expert).
Alternativ lassen sich die Wahrheitstafeln auch mit Hilfe eines Propeller Controllers P2 aufnehmen. Wie das geht, wird hier an Hand verschiedener Gatter exemplarisch gezeigt -> Übung 2.
Für die sechs Grundgatter gilt:
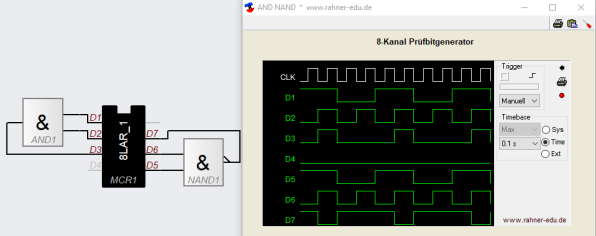
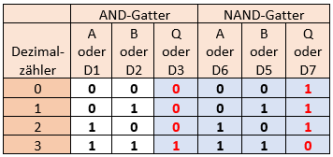
NAND- und AND-Gatter
Die boolesche Gleichung für ein AND-Gatter lautet: Q = A * B
Die boolesche Gleichung für ein NAND-Gatter lautet: Q = (A * B)´
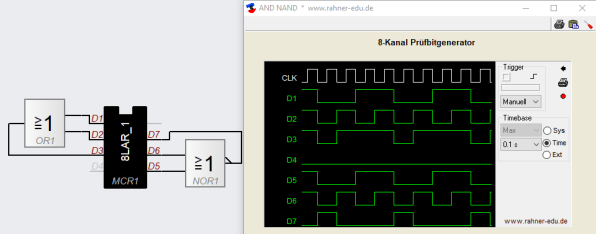
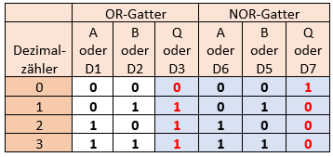
OR- und NOR-Gatter
Die boolesche Gleichung für ein OR-Gatter lautet: Q = A + B
Die boolesche Gleichung für ein NOR-Gatter lautet: Q = (A + B)´
XOR- und INV-Gatter
Die boolesche Gleichung für ein XOR-Gatter lautet: Q = (A´ * B) + (A * B´).
Die boolesche Gleichung für ein INV-Gatter lautet: Q = A´.
Das Apostroph bezeichnet das Inverse von A, auch als /A geschrieben. Die Multiplikation deutet auf AND-Gatter, die Addition auf OR-Gatter hin.
2 - Gesetze der Schaltalgebra
Kommutativgesetz (Vertauschungsgesetz)
Die Schaltvariablen einer AND- oder OR-Verknüpfung sind kommutativ; d.h., ihre Anschlüsse sind vertauschbar.
- AB = BA und A + B = B + A
Assoziativgesetz (Verbindungsgesetz)
Bei einer AND- oder OR-Verknüpfung mit mehr als zwei Eingängen pro Gatter ist die Reihenfolge, in der die Schaltvariablen verknüpft werden, beliebig.
- A(BC) = (AB)C = (AC)B = ABC (der Malpunkt zwischen den Buchstabentermen wurde hier weggelassen)
- A + (B + C) = (A + B) + C = (A + C) + B = A + B + C
Distributivgesetz (Verteilungsgesetz)
Wie in der Algebra gilt auch in der boolschen Algebra das Verteilungsgesetz.
- (AB) + (AC) = A(B + C)
Dies lässt sich mit einer entsprechenden Schaltung sofort überprüfen.
Für die linke Seite der Gleichung gilt: die Anschlüsse A und B sowie A und C sind UND-verknüpft (Multiplikation) und werden anschließend ODER-verbunden (Addition).
Für die rechte Seite der Gleichung gilt: B und C sind ODER-verknüpft; das Ergebnis davon wird mit A UND-verknüpft. Wenn die Gleichung stimmt, müssen die Zustandsdiagramme beider Schaltungen identisch sein (s. Abb. 4).
Weitere Gesetze der boolschen Algebra, die sich ebenfalls mit Hilfe von Zustandsdiagrammen überprüfen lassen, sind:
Komplementgesetz
- A + A´ = 1
- A * A´ = 0
Idempotenzgesetz
- A + A = A
- A * A = A
- A´´ = A
Gesetz vom kleinsten und größten Element
- A + 0 = A
- A + 1 = 1
- A * 0 = 0
- A * 1 = A
Mit Hilfe von Zustandsdiagrammen lassen sich De Morgansche Identitäten schnell überprüfen. Zwei Beispiele sollen das zeigen.
De Morgansche Identitäten
- (A * B)´ = A´ + B´
- (A + B)´ = A´ * B´
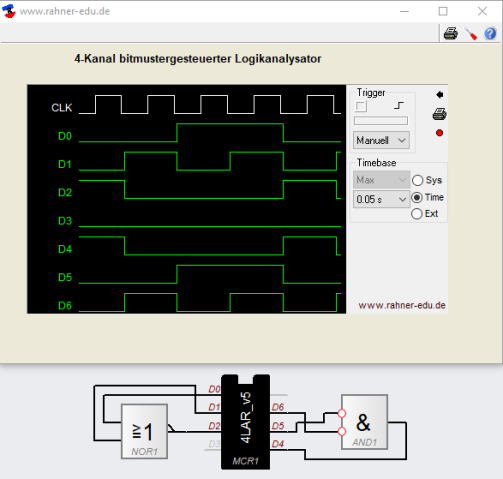
In Gleichung 1 sind auf der linken Seite A und B UND-verknüpft und das Ergebnis wird anschließend negiert. Auf der rechten Seite sind die negierten Anschlüsse A und B ODER-verknüpft.
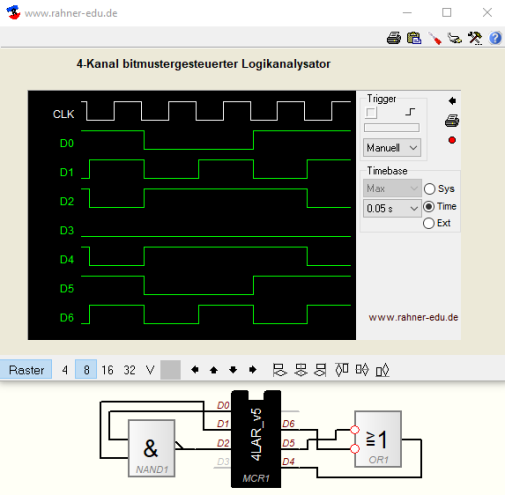
Die folgende Abbildung zeigt sowohl den diskreten Schaltungsaufbau als auch die Zustandsdiagramme der schaltungstechnischen Umsetzung der beiden De Morgan-Identitäten.
Ergebnis: Ein am Ausgang negiertes AND-Gatter verhält sich so wie ein an den Eingängen negiertes OR-Gatter.
Ergebnis: Ein am Ausgang negiertes OR-Gatter verhält sich wie ein an allen Eingängen negiertes AND-Gatter.
Schauen wir uns eine letzte Identität an und überprüfen sie anschließend mit dem Logikanalysator:
- (A + B) * (A + C) = A + (B * C)
Enthalten über eine AND-Verknüpfung verbunden OR-Verknüpfungen eine gleiche Schaltungsvariable (in diesem Beispiel ist es die Größe A), dann lässt sie sich ausklammern.
Mit diesem Rüstzeug sollten wir jetzt in der Lage sein,
- einfache digitale Schaltnetze sowohl umfassend zu untersuchen (Analyse oder Reengineering), was so viel heißt wie, die logischen Funktionen und Strukturen einer Schaltung umfassend offenzulegen und die Wahrheitstafel bzw. Funktionstabelle der Schaltung aufzustellen, als auch
- eine digitale Schaltung, die eine bestimmte Aufgabe genau erfüllen soll, zu entwickeln (Synthese).
3 - Analyse von Schaltnetzen
Hat eine Schaltung n Eingangsgrößen, dann gibt es 2n Ausgangsgrößen. Es liegt deshalb nahe, dass wir uns nur mit "kleinen" Schaltnetzen beschäftigen werden.
Logische Gatter mit zwei Eingangskanälen A und B haben immer 22= 4 Ausgangsgrößen. Die Wahrheitstafel wird dabei immer so aufgestellt, dass man von 0 beginnend dual hochzählt, das vereinfacht später die Vergleichbarkeit.
Übung 1
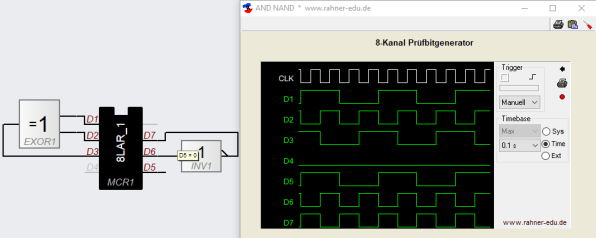
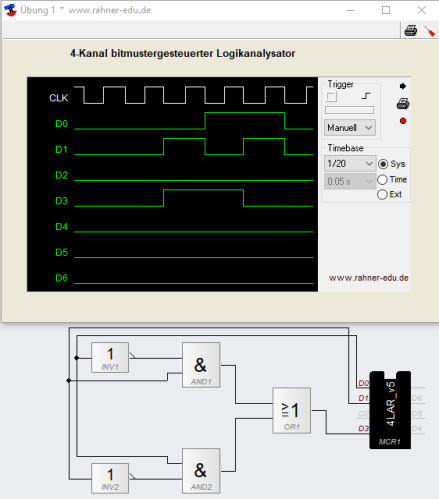
Es wird eine unbekannte Schaltung analysiert; als Hilfe dazu dient das Zustandsdiagramm (s. Abb. 7).
Lösung
Aus dem Schaltungsaufbau lässt sich die folgende boolesche Gleichung aufstellen:
- Q = (A´ * B) + (A * B´)
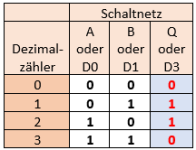
Die Auswertung des Zustandsdiagramms ergibt folgende Wahrheitstafel:
Die vorliegende Wahrheitstafel entspricht der eines XOR-Gatter (vergleiche dazu Abschnitt 1 - Schaltalgebra - XOR- und INV-Gatter auf dieser Seite). Das Schaltnetz lässt sich – bei gleicher Funktionalität – durch ein XOR-Gatter ersetzen.
Übung 2
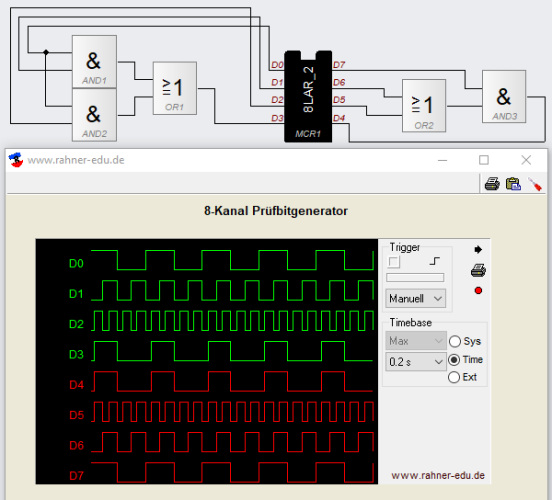
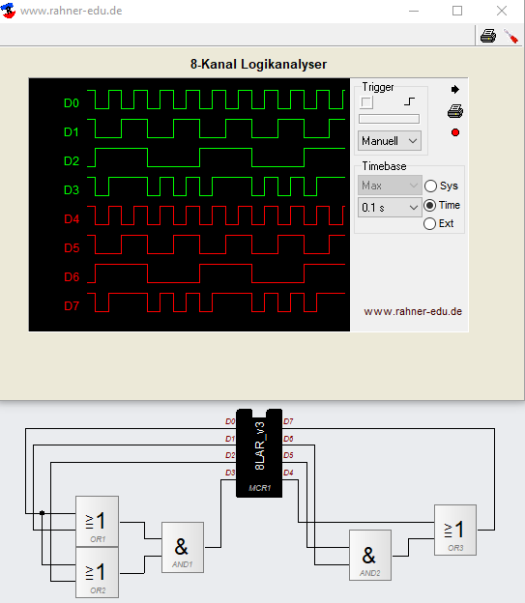
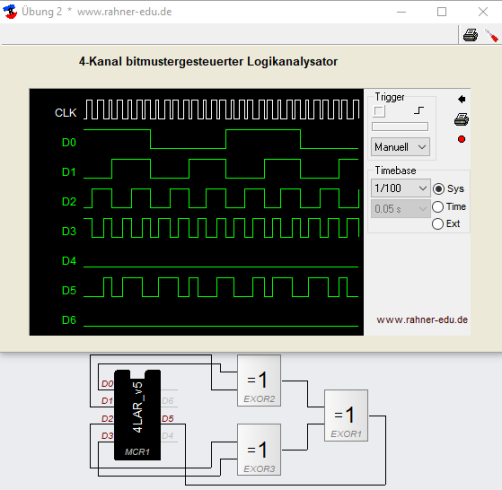
Die Schaltung in dieser Übung besteht aus drei XOR-Gattern (s. Abb. 8) und verfügt über vier Eingänge. Damit ergeben sich 16 mögliche Ausgangszustände. Das Verhalten des Schaltnetzes soll analysiert werden.
Wahrheitstafel aufstellen
| # |
Eingang A B C D |
Ausgang Q |
Gleichung bei einer "1" am Ausgang |
| 0 | 0 0 0 0 | 0 | |
| 1 | 0 0 0 1 | 1 | A´ B´ C´ D |
| 2 | 0 0 1 0 | 1 | A´ B´ C D´ |
| 3 | 0 0 1 1 | 0 | |
| 4 | 0 1 0 0 | 1 | A´ B C´ D´ |
| 5 | 0 1 0 1 | 0 | |
| 6 | 0 1 1 0 | 0 | |
| 7 | 0 1 1 1 | 1 | A´ B C D |
| 8 | 1 0 0 0 | 1 | A B´ C´ D´ |
| 9 | 1 0 0 1 | 0 | |
| 10 | 1 0 1 0 | 0 | |
| 11 | 1 0 1 1 | 1 | A B´ C D |
| 12 | 1 1 0 0 | 0 | |
| 13 | 1 1 0 1 | 1 | A B C´ D |
| 14 | 1 1 1 0 | 1 | A B C D´ |
| 15 | 1 1 1 1 | 0 |
Jedem HIGH- oder "1"-Signal am Ausgang lässt sich eine boolsche Gleichung zuordnen. Dies kann man in der Spalte "Gleichung bei einer ..." ablesen.
Wie man sofort erkennen kann, ist der Ausgang immer dann HIGH oder 1, wenn die Anzahl der Einsen, die an den Eingängen anliegen, ungerade ist (Odd-Parity-Check oder ungerade Prüfbit-Erzeugung).
Übung 3
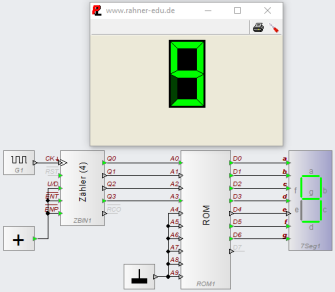
Mit einem Taktgeber, einem 4-Bit-Zählerbaustein, einer 7-Segment-Anzeige und einem ROM soll ein einstelliger Zähler (0 - 9) aufgebaut werden.
| Übung 3 - Aufbau eines Dezimalzählers von 0 - 9 | |
| Aufgabe |
|
| Material |
|
Schaltungsaufbau
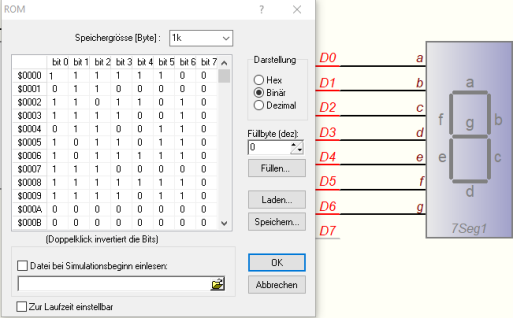
Bitmusterfolge im ROM
Verhalten der Zählschaltung
Es fällt auf, dass die Zählschaltung immer bis 16 hochzählt; das hat zur Folge, dass die Ziffernanzeige nach der 9 eine gewisse Zeit dunkel bleibt, bis der Zähler wieder bei 0 beginnt und die entsprechende Ziffer auf seinem Display darstellt.
Um das Dunkelschalten zu vermeiden, muss die Schaltung so abgewandelt werden, dass der Zähler mit Erreichen der Zahl 10 (0b1010) ein RESET durchführt.
RESET-Schaltung entwerfen
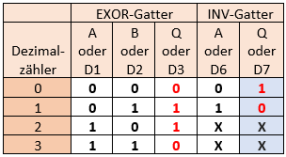
Gesucht ist eine Schaltung, die, sobald die Bitfolge 0b1010 erreicht ist, auf den Ausgang eine 0 oder 1 gibt (je nach Vorgabe, welcher Pegel am Zählerbaustein ein Reset auslöst; Datenblatt lesen) und damit ein Reset des Zählers auslöst.
Der Bitfolge 0b1010 entspricht der boolesche Term
- Q = AB´CD´
Benötigt wird ein AND-Gatter mit vier Eingängen; die Eingänge B und D werden invertiert.
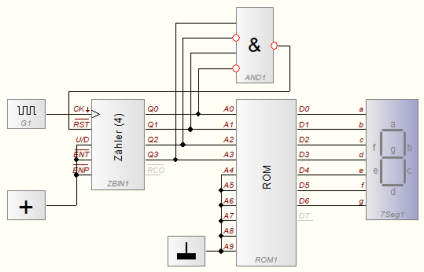
Die folgende Schaltskizze zeigt den modifizierten Versuchsaufbau.
Die Zählerschaltung funktioniert jetzt einwandfrei; sobald die Zahl 0b1010 erreicht ist, wird der Ausgang von AND1 auf 0 gesetzt und löst damit ein RESET des Zählers aus. Die binären Pseudotetraden (Dualzahlen > 0b1010) werden vom Zähler mit Hilfe des Resets übersprungen.