Digitaltechnik - 3
Codierer, Decodierer
3.1 - Dezimal-BCD-Codierer
An anderer Stelle wurde gezeigt, wie man mit einem Rechenwerk binäre Zahlen addiert und subtrahiert (Digitaltechnik - 1).
Die binäre Mathematik ist uns wenig geläufig, wir denken und rechnen normalerweise im Zehnersystem und so sind auch die Taschenrechner aufgebaut. Die Zahlen werden dezimal in den Rechner eingegeben, binär codiert, verarbeitet und am Ende wird das Ergebnis decodiert und als Zehner-Zahl wieder auf dem Display ausgegeben.
Es gibt eine Vielzahl von Codierern. Hier eine kleine Auswahl:
- Dezimal-zu-BCD
- Dezimal-zu-Aiken
- Dezimal-zu-Gray-Code
3.1.1 - BCD- oder 8-4-2-1-Code
Bei diesem gewichteten Code (jeder Stellenwert ist gewichtet) werden die Dezimalziffern von 0 bis 9 in einen binären 4-Bit-Code (ein Nibble) umgesetzt. Mit 4-Bit lassen sich aber maximal 16 Zahlen codieren. Die Dezimalzahlen 10 bis 16 werden nicht codiert und in der binären Darstellung als Pseudotetraden bezeichnet.
|
BCD-Code |
||||
|
8 |
4 |
2 |
1 |
Dezimal |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
2 |
|
0 |
0 |
1 |
1 |
3 |
|
0 |
1 |
0 |
0 |
4 |
|
0 |
1 |
0 |
1 |
5 |
|
0 |
1 |
1 |
0 |
6 |
|
0 |
1 |
1 |
1 |
7 |
|
1 |
0 |
0 |
0 |
8 |
|
1 |
0 |
0 |
1 |
9 |
|
1 |
0 |
1 |
0 |
10 |
|
1 |
0 |
1 |
1 |
11 |
|
1 |
1 |
0 |
0 |
12 |
|
1 |
1 |
0 |
1 |
13 |
|
1 |
1 |
1 |
0 |
14 |
|
1 |
1 |
1 |
1 |
15 |
Abb. 1 - BCD-Code. Jeder Dezimalzahl zwischen 0 und 9 wird ihre
binäre Darstellung zugeordnet. Alle Zuordnungen über 910 werden
als Pseudotetraden bezeichnet und sind in der Tabelle rot markiert.
Zwei- oder mehrstellige Dezimalzahlen werden im BCD-Code immer ziffernweise codiert.
Beispiel
|
Dezimalzahl |
BCD-codiert |
|
9 |
1001 |
|
25 |
0010 0101 |
|
3038 |
0011 0000 0011 1000 |
Pro Ziffer sind 4 Bit, eine Tetrade oder ein Nibble notwendig. Für vierstellige Dezimalzahlen benötigt man dann 16-Bit-Worte, um sie in den BCD-Code umzuwandeln.
| Dezimal-zu-BCD-Codierer | |
| Aufgaben |
|
| Material |
|
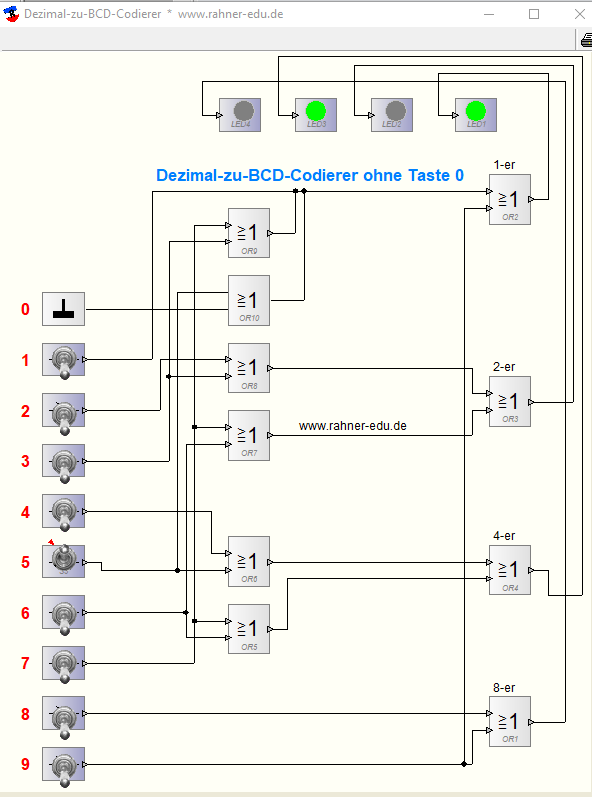
Schaltungsaufbau
Durch Überlegung und Probieren kann diese Schaltung relativ schnell aufgebaut werden.
3.2 - Dezimal-Aiken- oder 2-4-2-1-Codierer
Wie der BCD-Code ist auch dieser Code tetradisch, codiert die dezimalen Zahlen 0 bis 9 und ist symmetrisch aufgebaut. Das lässt sich am Besten an der Gegenüberstellung von Dezimalzahlen und Aiken-Code zeigen (siehe Tabelle 3).
|
Aiken-Code |
||||
|
2 |
4 |
2 |
1 |
Dezimal |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
2 |
|
0 |
0 |
1 |
1 |
3 |
|
0 |
1 |
0 |
0 |
4 |
|
0 |
1 |
0 |
1 |
Pseudo- tetraden |
|
0 |
1 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
|
|
1 |
0 |
1 |
0 |
|
|
1 |
0 |
1 |
1 |
5 |
|
1 |
1 |
0 |
0 |
6 |
|
1 |
1 |
0 |
1 |
7 |
|
1 |
1 |
1 |
0 |
8 |
|
1 |
1 |
1 |
1 |
9 |
Tabelle 3.2.1 – Funktionstabelle zum Aiken-Code
Der Aiken-Code ist in den ersten vier Dezimalzahlen mit dem BCD-Code identisch. Es folgen sechs Pseudotetraden. Die letzten fünf Zahlencodes ergeben sich aus der Negation der fünf ersten Zahlencodes. Dabei gilt: 9 ist die Negation von 0, 8 die von 1, 7 die von 2, …
Mit Hilfe der Tabelle 3.2.1 lässt sich die digitale Schaltung für einen Dezimal-Aiken-Codierer finden.
3.3 - 1-aus-10-Decodierer
Die dezimalen Ziffern von 0 bis 9 werden in einem 1-aus-10-Decodierer durch 10 Bits dargestellt. Dabei gilt, dass jeweils nur ein Bit auf 1 gesetzt ist, während die restlichen n-1 Bits 0 sind.
Beispiel für 1-aus-10-Code
|
1-aus-10-Decodierer |
|||
|
# |
1-aus-10-Code
987 65 4 321 0 |
Eingang
DCBA |
Gleichung |
|
0 |
0000000001 |
0000 |
D´ C´ B´ A´ |
|
1 |
0000000010 |
0001 |
D´ C´ B´ A |
|
2 |
0000000100 |
0010 |
D´ C´ B A´ |
|
3 |
0000001000 |
0011 |
D´ C´ B A |
|
4 |
0000010000 |
0100 |
D´ C B´ A´ |
|
5 |
0000100000 |
0101 |
D´ C B´ A |
|
6 |
0001000000 |
0110 |
D´ C B A´ |
|
7 |
0010000000 |
0111 |
D´ C B A |
|
8 |
0100000000 |
1000 |
D C´ B´ A´ |
|
9 |
1000000000 |
1001 |
D C´ B´ A |
|
10 |
|
1010 |
D C´ B A´ |
|
11 |
|
1011 |
D C´ B A |
|
12 |
|
1100 |
D C B´ A´ |
|
13 |
|
1101 |
D C B´ A |
|
14 |
|
1110 |
D C B A´ |
|
15 |
|
1111 |
D C B A |
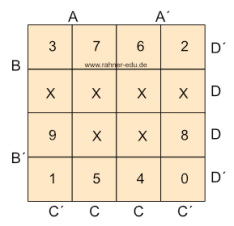
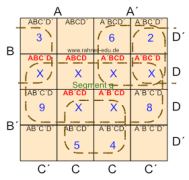
Die sechs redundanten Don´t-Care-Felder sind rot markiert und werden mit einem X in die KV-Tafel eingetragen; alle restlichen Positionen werden ebenfalls in die KV-Tafel übertragen.
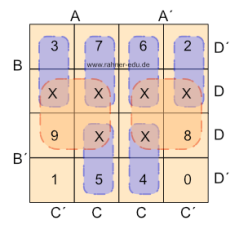
Mit der Nachbarschaftsregel KV4 ergibt sich dann die folgende KV-Tafel.
Abb. 4 entnimmt man die Ausgangsgleichungen für den 1-aus-10-Decodierer. Für die Ziffern 0 und 1 ist keine Minimierung möglich.
|
Ziffer |
Ausgangsgleichung |
|
0 |
A´ B´ C´ D´ |
|
1 |
A B´ C´ D´ |
|
2 |
A´ B C´ |
|
3 |
A B C´ |
|
4 |
A´ B´ C |
|
5 |
A B´ C |
|
6 |
A´ B C |
|
7 |
A B C |
|
8 |
A´ D |
|
9 |
A D |
Tabelle 1 – Aufstellung der Ausgangsgleichungen für
die zehn Ziffern von 0 bis 9 an Hand der KV4-Tafel aus Abb. 2.
Mit Hilfe von Tabelle 1 wird jetzt die Schaltung aufgebaut.
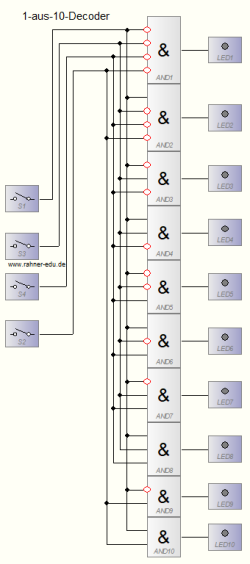
Schaltungsaufbau
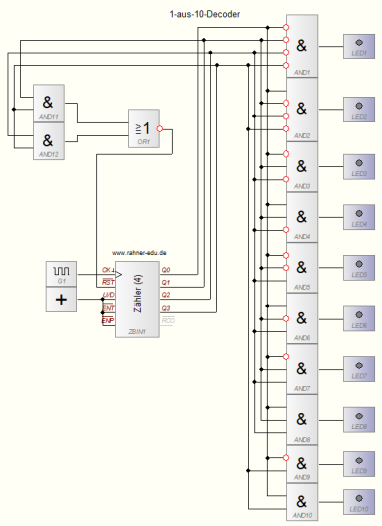
Abb. 5 – 1-aus-10-Decoder. Die 10 LEDs werden von oben nach unten „durchgeschaltet“, so wie es der Code vorsieht. Es leuchtet immer nur eine Diode. Um MIR die Arbeit zu erleichtern, habe ich in der Schaltung statt eines INV-Gatters die Eingänge negiert und Gatter mit unterschiedlich vielen Eingängen verwendet. Das erhöht auch die Übersichtlichkeit?
Bemerkung
Für die binäre Bitfolge von 0 bis 9 leuchten nacheinander die LEDs auf und es leuchtet immer nur eine LED.
Tauscht man die vier Eingangsschalter gegen einen 4-Bit Zählerbaustein aus, dann sieht das Ergebnis erwartungsgemäß anders aus. Der Zähler zählt von 0 bis 16; für alle binären Zahlen größer als 0b1001 ist im Schaltnetzwerk keine Beschränkung eingebaut. Mit der Folge, dass beim Zählen über 910 hinaus mehrere LEDs aufleuchten.
Dieser Fehler muss noch behoben werden. Die Überlegung dazu ist, eine Schaltung zu entwerfen, die immer dann, wenn eine Pseudotetrade aufgerufen wird, den Zähler zurücksetzt (RESET).
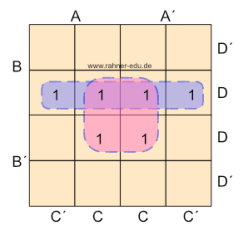
KV4-Tafel für Pseudotetraden aufstellen
Als Ausgangsgleichung ergibt sich aus der KV4-Tafel der Abb. 4:
- Q = B D + C D
Die zugehörige Schaltung zur Erkennung der Pseudocodes wird in die Schaltung aus Abb. 3 eingebaut.
Starte man jetzt das Programm neu, werden die LEDs über den 1-aus-10-Decoder nacheinander eingeschaltet und dies geschieht fortlaufend, weil nach 0b1001 (910) ein Reset ausgelöst wird und der Zähler neu startet.
Schaltungsaufbau mit Erkennung von Pseudotetragen und Auslösung eines Resets
3.2 - 7-Segment-Decodierer
In Übung 3 des Kapitels Digitaltechnik – 1 wurde gezeigt, wie man eine 7-Segment-Anzeige über einen 4-Bit Zähler mit ROM zu einer Zählschaltung ausbaut.
Mit Hilfe der Segmentidentifizierung bei einem 7-Segment-Display und der Zifferndarstellung lässt sich eine Funktionstabelle für die Funktionsentwicklung eines 7-Segment-Decodierers aufstellen (siehe hierzu auch unter
- AVR-Controller und BASCOM: 7-Segment-LED Anzeige,
- BASIC Stamp 2 – 7-Segment-Anzeige und
- Propeller Controller – 7-Segment-Anzeige).
Mit einer 7-Segment-Zifferanzeige lassen sich die Zahlen 0 bis 9 darstellen. Die einzelnen LED-Segmente sind beschriftet und über Elektroden nach außen geführt. In der Funktionstabelle sind die Eingangs- und Ausgangsbelegungen aufgeführt.
|
Zahl |
Eingang
D C B A |
Ausgang LED-Segment a b c d e f g |
|
0 |
0 0 0 0 |
1 1 1 1 1 1 0 |
|
1 |
0 0 0 1 |
0 1 1 0 0 0 0 |
|
2 |
0 0 1 0 |
1 1 0 1 1 0 1 |
|
3 |
0 0 1 1 |
1 1 1 1 0 0 1 |
|
4 |
0 1 0 0 |
0 1 1 0 0 1 1 |
|
5 |
0 1 0 1 |
1 0 1 1 0 1 1 |
|
6 |
0 1 1 0 |
1 0 1 1 1 1 1 |
|
7 |
0 1 1 1 |
1 1 1 0 0 0 0 |
|
8 |
1 0 0 0 |
1 1 1 1 1 1 1 |
|
9 |
1 0 0 1 |
1 1 1 1 0 1 1 |
Im nächsten Schritt muss für jedes LED-Segment ein KV-Diagramm erstellt und anschließend minimiert werden. Dazu sollen auch die Pseudotetraden eingebunden werden. Für die beiden LED-Segmente e und f lauten die Gleichungen beispielsweise:
e-Segment
- e = A´ B´ C´ D´ + A´ B C´ D´ + A´ B C D´ + A´ B´ C´ D
f-Segment
- f = A´ B´ C´ D´ + A´ B C´ D´ + A´ B C´ D + A´ B C D´ + A B´ C´ D´ + A B´ C´ D
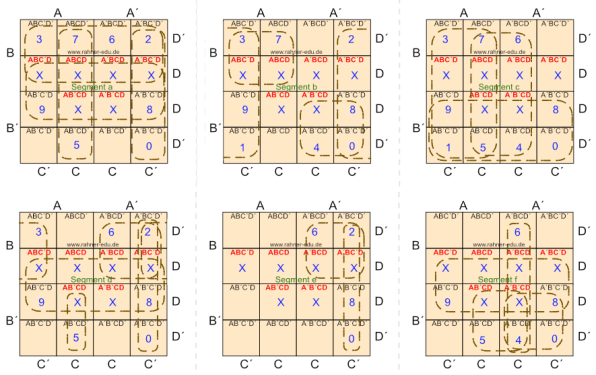
In den nachfolgenden KV-Diagrammen sind die Segmente und die Ziffern, in denen sie eingeschaltet werden, dargestellt.
KV-Diagramme
Zu jedem KV-Diagramm muss die Gleichung für das jeweilige Segment aufgestellt werden. Das ist ein mühsamer Prozess, der sehr fehleranfällig ist. Es ergeben sich die folgenden sieben Gleichungen:
- Segment a = D + B + AC + A´ C´
- Segment b = AB + A´ B´ + C´ + D
- Segment c = C + B´ + A + D
- Segment d = D + B C´ + A´ B + A B´ C + A´ C´
- Segment e = A´ B + A´ C´ + BD + CD
- Segment f = D + A´ C + B´ C + A´ B´
- Segment g = D + B´ C + A´ B + B C´
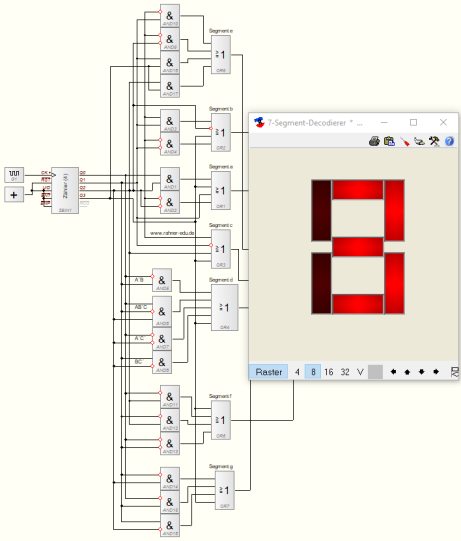
Schaltungsaufbau