1 - Binäres Zahlensystem oder 2-er System
In Analogie zum Zehnersystem, das ist das uns geläufige Zahlensystem, ist ein 2-er System oder auch Binärsystem aufgebaut.
2 - Das Stellenwertsystem
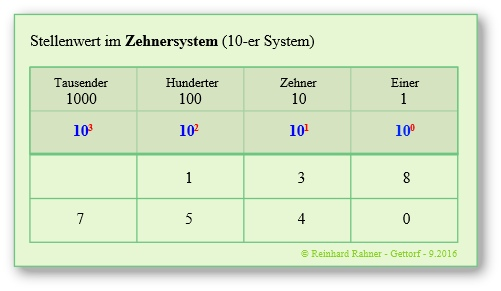
Das Zehnersystem ist ein sogenanntes Stellenwertsystem. Das heißt, dass die Position einer Ziffer innerhalb einer Zahl einen bestimmten festen Stellenwert hat. Dieser richtet sich nach dem jeweiligen Zahlensystem und wird in Potenzen des jeweiligen Zahlensystems ausgedrückt.
Im 10-er System sind die Stellenwerte als Potenzen der Zahl 10 dargestellt, im 2-er System als Potenzen der Zahl 2 und im 16-er System als Potenzen der Zahl 16.
Die Zahl 138 setzt sich zum Beispiel zusammen aus einem Hunderter, drei Zehnern und acht Einern oder mathematisch ausgedrückt:
-
138 = 1 x 102 + 3 x 101 + 8 x 100
Entsprechend setzt sich die Zahl 7540 zusammen aus
-
7540 = 7 x 103 + 5 x 102 + 4 x 101 + 0 x 100
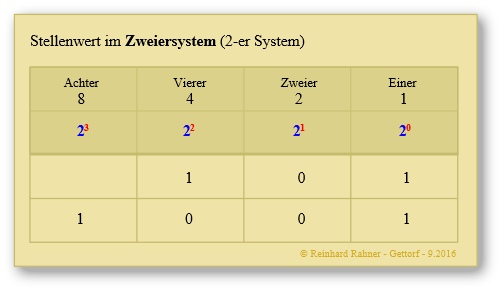
Man erkennt, dass die Stellenwerte von rechts nach links jeweils um eine Potenz zunehmen. Ganz rechts stehen die Einer, als 10-er Potenz geschrieben: 100. Links daneben stehen die Zehner oder als 10-er Potenz geschrieben: 101. Übertragen wir das auf das Binärsystem, dann ergibt sich in Analogie entsprechend:
Die Zahl 10012 setzt sich aus einem Achter, Null Vierer, Null Zweier und einem Einer zusammen. Mathematisch ausgedrückt:
-
10012 = 1 x 23 + 0 x 22 + 0 x 21 + 1 x 20
Die tief gestellte 2 soll darauf hinweisen, dass es sich um eine Binärzahl handelt und nicht um die Zahl 1001 aus dem Zehnersystem. Die zweite Binärzahl lässt sich nun entsprechend schreiben:
-
1012 = 1 x 22 + 0 x 21 + 1 x 20
Häufig wird die tief gestellte 2 weg gelassen; um deutlich zu machen, dass es Binärzahlen sind, werden die Ziffern etwas anders geschrieben: I und O statt 1 und 0.
3 - Hexadezimales System oder 16-er System
In Analogie zum 2-er und 10-er System ist das 16-er System aus 16 Ziffern aufgebaut.
Den Aufbau des Stellenwertsystem eines 16-er Systems zeigt die folgende Abbildung.
Die Zahl F816 (16-er System) setzt sich zusammen aus
-
F x 161 + 8 x 160 = 15 x 161 + 8 x 160
Das entspricht der Zahl 248 im Zehnersystem. Entsprechend lässt sich die Hexadezimalzahl 10A416 umrechnen:
-
1 x 163 + 0 x 162 + A x 161 + 4 x 160
Das entspricht der Zahl 4260 im 10-er System.
Wie man erkennen kann, benötigt man im 16-er System relativ wenig Stellen, um große Zahlen darzustellen und relativ viele Stellen im 2-er System.